
 |
 |
![]()
For printing, download the pdf version.
![]()
A Comparison of Different Cognitive Paradigms
Using Simple Animats in a Virtual Laboratory,
with Implications to the Notion of Cognition
Carlos Gershenson
Advisor: Chris Thornton
Abstract
In this thesis I present a virtual laboratory which implements five different models for controlling animats: a rule-based system, a behaviour-based system, a concept-based system, a neural network, and a Braitenberg architecture. Through different experiments, I compare the performance of the models and conclude that there is no “best” model, since different models are better for different things in different contexts. The models I chose, although quite simple, represent different approaches for studying cognition. Using the results as an empirical philosophical aid, I note that there is no “best” approach for studying cognition, since different approaches have all advantages and disadvantages, because they study different aspects of cognition from different contexts. This has implications for current debates on “proper” approaches for cognition: all approaches are a bit proper, but none will be “proper enough”. I draw remarks on the notion of cognition abstracting from all the approaches used to study it, and propose a simple classification for different types of cognition.
A la memoria de mi abuelo
Acknowledgements
I want to thank my advisor Chris Thornton and my teachers at Sussex University, Inman Harvey, Ezequiel Di Paolo, Andy Clark, Josefa Toribio, Emmet Spier, David Young, and Phil Husbands for their knowledge, time, patience, and advices.
My classmates, especially Marcello Ghin, Xabier Barandiaran, Chrisantha Fernando, Hywel Williams, Eldan Goldenberg, Will Coates, Billy Shipp, Vasco Castela, and Peter Law, gave me valuable comments and suggestions. Also the E-Intentionality, ALERGIC, and LOINAS groups at the School of Cognitive and Computer Sciences provided valuable ideas and feedback.
I also give thanks to Peter Gärdenfors, Christian Balkenius, and the people from LUCS; Francis Heylighen, Alex Riegler, and the people from CLEA; Rodney Brooks, Kevin O’Regan, Christopher Prince, Andy Wuensche, Gottfried Mayer-Kreiss, Jason Noble, Richard Watson, Jelle Zuidema, Uri Hershberg, Paul Fitzpatrick, Terrence Stewart, Josh Bongard, and Anil Seth, for interesting discussions that helped me greatly in developing my ideas.
I should also give thanks to my all-time teachers and friends in México, especially José Negrete, Pedro Pablo González, Jaime Lagunez, and Javier Fernández Pacheco, for the invaluable bases I received from them.
I thank my parents and family for their endless support and motivation.
Надя... без тебя это было бы невозможно... спасибо за все.
My studies were supported in part by the Consejo Nacional de Ciencia y Tecnología (CONACYT) of México.
Table of Contents
3.1. Survival in a scarce environment.
3.2. Survival in an abundant environment.
3.3. Individual survival in environment of fixed resources.
3.4. Discrimination of stimulus value
4.2. Equivalence of different models
4.5. Different types of cognition
7. Appendix A: KEBA description
8. Appendix B: Virtual Laboratory Specification
“All human knowledge, up to the highest flights of science,
is but the development of our inborn animal instincts.”
—Charles Sanders Peirce (1932, p. 477)
The initial goal of this work was to show that knowledge can be developed by a cognitive system parting from adaptive behaviour. My aim was to do this by building artificial systems which develop in such a way that they exhibit knowledge, but not implemented directly. After a relatively easy success of my goal, I stumbled with an interpretational problem: adaptive behaviour can be seen as a form of knowledge, but also vice versa. So how can we know of the system really acquired knowledge, or if it were just conditioning, when the same process can be described from both perspectives?
I decided to try to clarify these issues by going deeper into basic notions of cognitive science. What can we consider being cognition? Cognition comes from the Latin cognoscere, which means ‘get to know’. We can say that cognition consists in the acquisition of knowledge. We can say that a system is cognitive if it knows something. Humans are cognitive systems because they know how to communicate, build houses, etc. Animals are cognitive systems because they know how to survive. Autonomous robots are cognitive systems if they know how to navigate. Does a tree know when spring comes because it blossoms? We should better slow down, these issues will be discussed in Section 4.
In classical cognitive science and artificial intelligence (e.g. Newell and Simon, 1972; Newell, 1990; Shortliffe, 1976; Fodor, 1976; Pylyshyn, 1984; Lenat and Feigenbaum, 1992), people described cognitive systems as symbol systems (Newell, 1980). However, it seemed to become a consensus in the community that if a system did not used symbols or rules, it would not be cognitive. From this perspective, animals are not cognitive systems because they do not use and have symbols. Nevertheless, if we open a human brain, we will not find any symbol either. Opposing the symbolic paradigm, the connectionist approach was developed (Rumelhart, et al., 1986; McClelland, et al., 1986), assuming that cognition emerges from the interaction of many simple processing units or neurons. To my knowledge, there has been no claim that “therefore a cognitive system should be able to perform parallel distributed processes, otherwise it is not cognitive”. Still, there has been a long discussion on which paradigm is the “proper” one for studying cognition (Smolensky, 1988; Fodor and Pylyshyn, 1988). The behaviour-based paradigm (Brooks, 1986; 1991; Maes, 1994) was developed also opposing the symbolic views, and not entirely different from the connectionist. There have been also other approaches to study cognition (e.g. Maturana and Varela, 1987; Beer, 2000; Gärdenfors, 2000).
The actual main goal of this work is to show that there is no single “proper” theory of cognition, but different theories that study cognition from different <perspectives|contexts> and with different goals. Moreover, I argue that in theory any cognitive system can be modelled to an arbitrary degree of precision by most of the accepted theories, but none can do this completely (precisely because they are models). I believe that we will have a less-incomplete understanding of cognition if we use all the theories available rather than trying to explain every aspect of cognition from a single perspective.
This view is currently shared by many researchers, but to my knowledge, there has been no empirical study in order to backup these claims. For achieving this, I implemented different models from different paradigms in virtual animats, in order to compare their cognitive abilities. The models I use are not very complex, not to at all to be compared with humans, but they are useful for understanding the generic processes that conform a cognitive system. After doing several comparative experiments, I can suggest, using the simulation results as a philosophical aid, that there is no “best” paradigm, and each has advantages and disadvantages.
In the following section, I present a virtual laboratory developed in order to compare
the implementations in animats of models coming from five different perspectives: rule-based
systems
![]() , behaviour-based systems, concept-based systems, neural networks, and Braitenberg
architectures. Because of space limitations, I am forced to skip deep introductions to each
paradigm for studying cognition, but the interested reader is referred to the proper material.
In Section 3, I present experiments in order to compare the performance of the animats in
different scenarios. With my results, in Section 4 I discuss that each model is more appropriate
for modelling different aspects of cognition, and that there is no “best” model. I also discuss
issues about models, and from my results I try to reach a broader notion of cognition merging
all the paradigms reviewed. I also propose a simple classification of different types of cognition.
In the Appendixes, the reader can find details about the original concept-based model I use
and about my virtual laboratory.
, behaviour-based systems, concept-based systems, neural networks, and Braitenberg
architectures. Because of space limitations, I am forced to skip deep introductions to each
paradigm for studying cognition, but the interested reader is referred to the proper material.
In Section 3, I present experiments in order to compare the performance of the animats in
different scenarios. With my results, in Section 4 I discuss that each model is more appropriate
for modelling different aspects of cognition, and that there is no “best” model. I also discuss
issues about models, and from my results I try to reach a broader notion of cognition merging
all the paradigms reviewed. I also propose a simple classification of different types of cognition.
In the Appendixes, the reader can find details about the original concept-based model I use
and about my virtual laboratory.
Following the ideas presented in Gershenson, González, and Negrete (2000), I
developed a virtual laboratory for testing the performance of animats controlled by
mechanisms proposed from different perspectives
![]() in a simple virtual environment.
Programmed in Java with the aid of Java3D libraries, this software is available to the public,
source code and documentation included, at https://bingweb.binghamton.edu/%7Ecgershensong/unamcogs/keb.
in a simple virtual environment.
Programmed in Java with the aid of Java3D libraries, this software is available to the public,
source code and documentation included, at https://bingweb.binghamton.edu/%7Ecgershensong/unamcogs/keb.
In my virtual laboratory, the user can create different phenomena, such as rocks (grey cubes), food sources (green spheres), rain (blue semitransparent cylinders), lightnings (black cylinders), and spots of different colours (circles): randomly or in specific positions. These also can be generated randomly during the simulation at a selected frequency. Lightnings turn into rain after ten time steps, and rain turns into food after fifty time steps.
All the animats have an energy level, which decreases when their hunger or thirst are high, and is increased when these are low (energy, thirst, hunger ∈ [0..1]). An animat dies if its energy is exhausted. Eating food decreases their hunger. They can decrease their thirst by drinking under rains. Hunger and thirst are increased if they attempt to drink or eat “incorrect” stimuli. They lose energy if they touch lightnings or rocks. Basically, an animat in order to survive just needs to eat when hungry, drink when thirsty, and avoid lightnings and rocks. We can say that they are cognitive systems if they are successful, because they would know how to survive. The animats can leave a coloured trail in order to observe their trajectories. We can appreciate screenshots of the virtual environment in Figure 1 and Figure 2. A detailed technical description of the implementation of my virtual laboratory can be found in Appendix B.
 Figure 1. Virtual environment, ground view.
Figure 1. Virtual environment, ground view.
 Figure 2. Virtual environment, aerial view.
Figure 2. Virtual environment, aerial view.
There are many models that would solve the problem of surviving is such an environment, but I decided to implement representative models of different paradigms in order to observe their differences and similitudes. These models are as follows: a rule-based system typical of traditional knowledge-based and expert systems (e.g. Newell and Simon, 1972); Maes’ (1990, 1991) action selection mechanism, an already classical behaviour-based system (Brooks, 1986; Maes, 1994); my original architecture of recursive concepts as an example of the novel concept-based approach (Gärdenfors, 2000); a simple feed-forward artificial neural network (for an introduction, see Arbib, 1995); and a Braitenberg-style architecture (Braitenberg, 1984).
“For anything to happen in a machine some process must know enough to make it happen.”
—Allen Newell
Rule-based animats have perceptual and motor functions that ignore the problems of implementing perception and motion in physical agents, focussing only in the control mechanism. They are inspired in classical knowledge-based systems (Newell and Simon, 1972; Newell, 1990), which use logic rules manipulating symbols in order to control a system. Table 1 shows the rules that control the animats in their environment.
if (rockNear OR lightningNear) then{
avoid
}else if ((thirst>=0.1) AND (rainPerceived)) then{
if (rainAtRange) then{
drink
}else{
approachRain
}
}else if ((hunger>=0.1) AND (foodPerceived)) then{
if (foodAtRange) then{
eat
}else{
approachFood
}
}else if ((thirst>=0.1) AND (lightningPerceived)) then{
approachLightning
}else if ((hunger>=0.1) AND (rainPerceived)) then{
approachRain
}else if ((thirst>=0.1) OR (hunger>=0.1)) then{
explore
}else{
noAction
}
If rule-based animats perceive a rock near them, they avoid it. If they are thirsty and perceive rain, then if they can reach it drink, otherwise approach to it, and so on. They approach lightnings when thirsty and rains when hungry because “they know” that these will turn into rain and food respectively.
The perceptual system detects phenomena in all directions at a distance lesser than the adjustable animat’s radius of perception, detects phenomena near when they are at a distance lesser than the radius of the animat’s body, and detects phenomena at range when the animat touches them. The motor system approaches phenomena in a straight line, explores with random movements, and avoids obstacles semi-randomly turning about + or - 90 degrees.
Knowledge-based systems have several limitations (e.g. see Maes, 1994), and are not optimal for implementing different types of system, but they are suitable for this task. We could see them as models of cognizers, even humans, which in such conditions would deliberately take those decisions. Classical cognitive science argues that humans are cognitive systems because they use rules and reasoning as the ones these animats could model (e.g. Newell, 1990).
Maturana and Varela give the following definition: “behaviour is a description an observer makes of the changes in a system with respect to an environment with which the system interacts” (Maturana and Varela, 1987, p. 163). We should just remember that behaviours are defined by an observer.
Behaviour-based systems (Brooks, 1986; Maes, 1994) have been inspired in ethology for modelling adaptive behaviour and building adaptive autonomous agents. In problem domains where the system needs to be adaptive, they have several advantages over knowledge-based systems (Maes, 1994). But when it comes to modelling the type of cognition that knowledge-based systems model, they have not produced any better results (Kirsh, 1991; Gershenson, 2002b).
I implemented Maes’ (1990; 1991) action selection mechanism (ASM) for controlling my behaviour-based animats. It consists of a network of behaviours. Each behaviour has an activation level, a threshold, and a set of conditions in order to be “executable”. An executable behaviour whose activation level surpasses the threshold becomes active. The creatures controlled by Maes’ ASM also have motivations such as hunger or safety, which also contribute to the activation of behaviours. The behaviours are connected through “predecessor”, “successor”, and “conflicter” links. There is a predecessor link between A and B (B precedes A) if B makes certain conditions of A come true. For example, “eat” has “approach food” as a predecessor. There is a matching successor link in the opposite direction for every predecessor link. There is a conflicter link from A to B if B makes a condition of A undone. Behaviours activate and inhibit each other, so after some time the “best” behaviour becomes selected. For details of this ASM, the reader is referred to Maes (1990; 1991).
As with the rule-based animats, here I also simplify perceptual and motor systems (actually using the same systems already described), since they take the form of procedures such as “food perceived” or “avoid obstacle”, and these systems have to deal with the problem of distinguishing food from non-food, or how to move in order not to crash. Figure 3 shows the behaviour network of the animats.
The external conditions of the behaviours are obvious: rock or lightning near for “avoid” , food perceived for “approach food”, food at range for “eat”, none for “explore”, etc. The internal motivations are safety (constant) for “avoid”, hunger for the ones related with food, thirst for the ones related with thirst, none for “approach lightning”, hunger, thirst and curiosity (constant) for “explore”, and boredom (constant) for “none”.
Curiously, the animats, even when they make discriminations between the highest motivations (approach food if more hungry than thirsty even if rain is closer), behave in a reactive way (eat when they are not hungry), because of the activation of behaviours by the successor links. Therefore, if the behaviour “none” is active for a long time, it will increase the value of “explore”, and this “approach rain” if this one is present, because thirst is not a direct condition. Of course, I could fix Maes’ ASM adding the motivations as a condition for a behaviour to become executable, or explore exhaustively the parameter space of the mechanism. This last option is not an easy one, since indeed it takes some time to adjust all the parameters by trial-and-error.
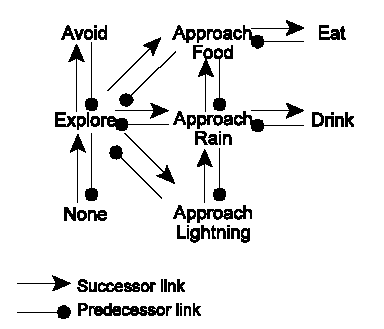 Figure 3. Behaviour network of behaviour-based
animats, based on Maes (1990; 1991).
Figure 3. Behaviour network of behaviour-based
animats, based on Maes (1990; 1991).
Concepts can be considered as discrete categorizations (Gärdenfors, 2000), as opposed to sensation and perception which can be considered as continuous categorizations. Concepts can be seen as a discretization of the perceptual space.
For the concept-based animats I used with minor improvements my original, previously developed, architecture (Gershenson, unpublished), named KEBA, where “concepts” are recursively generated from regularities of the sensors and of other concepts, and linked to actions by simple reinforcement learning. The activity of the concepts decides which action will be executed. First versions of my virtual laboratory were developed to test this architecture, and now I extended it in order to study all the animat types I present here. For a detailed description of KEBA, see Appendix A.
Actually, KEBA is not at all an optimal architecture in pragmatic terms, since it takes lots of effort in solving a problem which other architectures do quite easily. However, it was created with an explanatory role, trying to understand how concepts, and logic, could be developed from the interactions of an agent with its environment. One thing I have learned is the importance of the gradual development (Piaget, 1968; Balkenius et al., 2001) for acquiring proper performance in complex environments. The animats have a difficult time if they are set right into a random complex environment. Nevertheless, if we set them in simple environments, so that they can learn different tasks at different times, gradually, they perform better.
If we would be interested only in performance, we could define the concepts and manually link them to actions. However, that was not the intention, since it would easily work, but not better in any interesting way than simpler models.
Artificial neural networks (for an introduction, see Arbib, 1995) are mathematical models, which consist of interconnected “units” or “neurons” which have activation values. These values change accordingly to the state of the inputs to the network and to the connections between neurons. Neurons multiply their inputs by given weights (which can be adjusted by learning algorithms) and combine them accordingly to a specific function. They were not used at first for controlling autonomous agents, but they have proven to be useful for this purpose as well (e.g. Beer, 1996; Slocum, Downey, and Beer, 2000).
The neural animats have pairs of sensors for detecting food, rain, and rocks. Each sensor is on one side of the animat, so for example the left sensor for rain becomes active when there is rain on the left of the animat, and so on. For implementation purposes, we measure a ponderation ratio of the size of the phenomenon over its distance, so that for example larger objects at the same distance, or the closest of several objects of the same size, will cause a higher activity in the sensor. This would simulate the fact that for example if a lamp is very bright but farther than a close dim one, a photosensor in a real robot could react more to the far bright light. Each sensor perceives 180°, so that each pair of sensors is mutually exclusive and combining them the animats perceive 360°. They also have two motors (left and right), which simulate the movement of wheels. This setup is traditional of simulated and robotic experiments with kephera-like robots. In Figure 4 we can appreciate a diagram of the structure of these animats.
These animats use a three-layered feed-forward neural network for controlling their motors. The inputs of the network are the sensors and the internal motivations hunger and thirst. These activate eight input neurons, which combine their values for the inputs of six hidden neurons. Two output neurons determine the speed of the motors, which have small added random noise, in order to make the simulation a bit less unrealistic (Jakobi, Husbands, and Harvey, 1995). The neurons simply multiply their inputs by fixed weights and sum them. Then, the activation of the neuron will be this sum if it is higher than a threshold, and zero otherwise. We can see a diagram of this neural network in Figure 5.
Note that there is no learning in this specific neural network, which is one advantage of these models. Even so, they perform appropriately in their simple environment. Learning can allow animats to adapt to specific conditions of their environment (Gershenson and González, 2000).
If the animat is hungry or thirsty and touching a food source or rain, it eats or drinks, respectively. The consummatory “behaviours” (eat and drink) are independent of the motor activity. This causes that the animats cannot “stop and eat”, but only “eat on the go”.
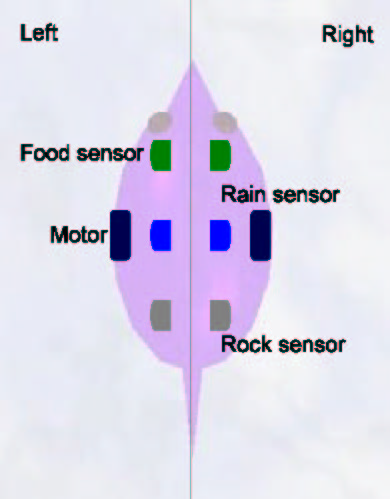 Figure 4. Motors and sensors of animats.
Figure 4. Motors and sensors of animats.
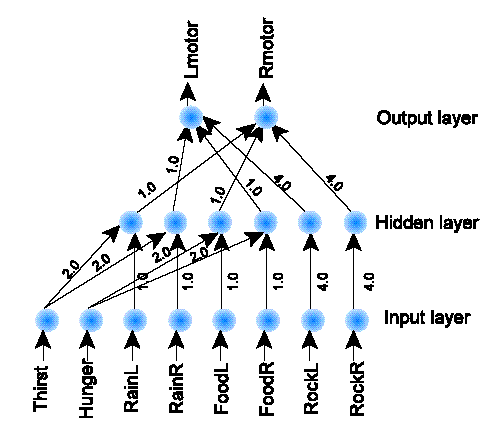 Figure 5. Network controlling neural animats.
Figure 5. Network controlling neural animats.
One advantage of solving the problem of survival at this level is that we are not predetermining behaviours as “approach food” or “avoid” in order to be selected (Seth, 1998), and the sensors are quite simple. Anyway, these animats also survive in their environment. One small issue is that since they move in zigzag because of their wheels, they take more time to reach, let us say a food source, than an animat with an implementation of “approach food” (following a straight line).
“Vehicles” are architectures introduced by Braitenberg (1984). They are autonomous agents with direct links from sensors to motors. One example is a two-wheeled robot with two light sensors. The left sensor is connected to the right motor, so that when there is more light on the left of the vehicle, the right motor turns faster. The right sensor is connected to the left motor. The behaviour this simple setup produces can be described as phototactic. If there is a light to the left of the vehicle, the left sensor will become more active than the right, and therefore the right motor will turn more than the left, and the vehicle will turn left (towards the light). This movement sets up the light source on the right of the vehicle, and then it will turn right. These sequences will make the vehicle approach to the light. Another simple example, if we connect the left sensor to the left motor and the right sensor to the right motor, then the vehicle will flee from light sources. Many interesting behaviours can be produced with several sensors and different connections. Braitenberg vehicles have been extended, among others, by Lambrinos and Scheier (1995) and by Seth (1998). The type of cognition exhibited by Braitenberg architectures can be compared with the one exhibited by W. Grey Walter’s tortoises (Walter, 1950; 1951).
My Braitenberg-style animats were handcrafted (i.e. not evolved). They have a similar setup as the neural network animats, shown in Figure 4: six sensors and two motors. There are direct links from the sensors to the motors, which have some small random noise: food and rain sensors are connected to the opposite motors (left to right, right to left), and rock sensors are connected to their corresponding motors (left to left, right to right). The speed of the motors is multiplied by the energy of the animats (slower when energy is low), and the links of food and rain sensors are multiplied with the values of hunger and thirst, respectively (faster when motivations are high). As with neural network animats, Braitenberg animats have independent consummatory behaviours: they eat if they are hungry while touching food and drink if thirsty while touching rain. Figure 6 shows the connection diagram of the Braitenberg animats.
With this simple setup, Braitenberg animats are able to survive successfully in their simple environment. The main idea is that they approach to food proportionally to their hunger, to rain proportionally to their thirst, but also flee from rocks when they are close enough, providing efficient obstacle avoidance. Because every sensor contributes to the motor speed, both motors compete in such a way to produce the optimal behaviour, without indecisions. Also, animats have noise in their motors proportional to their motivations, so when they are hungry or thirsty they move randomly at a speed proportional to their internal need, providing a kind of random exploration. This noise is also present when they are “approaching food” or any other behavioural description an observer could make, but this does not affect their final performance, since Braitenberg architectures are quite robust to noise.
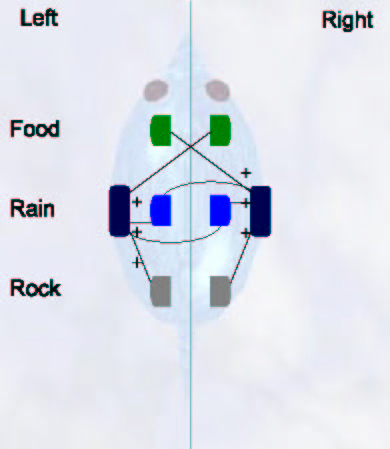 Figure 6. Direct connections of the
Braitenberg animats.
Figure 6. Direct connections of the
Braitenberg animats.
I have realized series of experiments in order to compare the different properties of the architectures which control each type of animat. The reader is invited to download my virtual laboratory and test the experiments I show here, and to devise her/his own.
I do not suggest that my simulations and experiments prove anything, but I think of them as an aid to present and produce ideas. I agree with the possible critic who would say that I am solving a toy problem, but most of the models, simulations or robots, do not go much farther (See Hallam et al. (2002) for recent work). And the only way they go farther is by adding more behaviours, stimuli, motivations, etc., but the degree of simplification is as terrible as the one I have here.
I could also be criticized by some arguing that my experiments are not “really cognitive”, because the animats do not have any kind of problem solving or symbol manipulation. This is not correct. Every animat needs to solve the problem of surviving in its environment (problems are determined by an observer). And rule-based animats can be said to be using the symbols received by their perceptual system. Another critic can be that this problem of survival is very simple and not “representation-hungry” (Clark and Toribio, 1995). As we will see in Section 4, these problems are possible to solve as well with architectures from different paradigms, but my ideas can be seen more clearly in this simple setup rather than in problem domains in which different architectures from different paradigms are specialized because of computational efficiency.
I present experiments for observing the performance of the animats in shared scarce and abundant environments. I also test the survival of the animats in individual environments of fixed resources. In these experiments I also use a “control” animat with random action selection. Then I test the ability of the animats to discriminate between the values of different stimuli, as an example of a simple relational task. Finally, I test how different animats can cope with conflicting goals. An experiment for testing KEBA is presented in Appendix A.1.
3.1. Survival in a scarce environment.
For this experiment, I set one animat of each type, and an animat with random action selection, with no initial internal needs and highest energy value. I set the ratio of random generation of phenomena to very low, making the rain and food scarce. Figure 7 shows the history of internal states of the animats for this scenario.
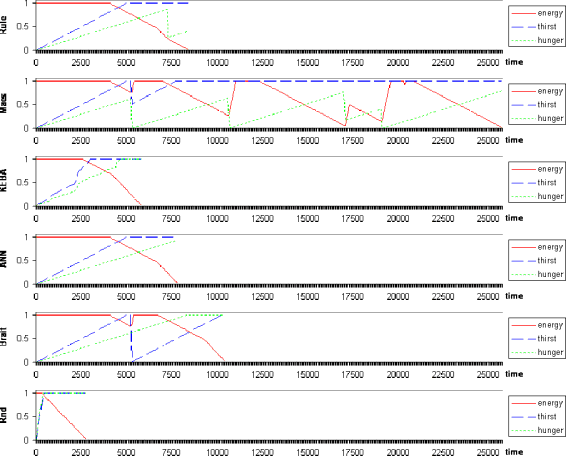 Figure 7. Animats dying in a scarce environment. Rule=rule-based, Maes=behaviour-based,
KEBA=concept-based, ANN=neural network, Brait=vehicle, Rnd=random
Figure 7. Animats dying in a scarce environment. Rule=rule-based, Maes=behaviour-based,
KEBA=concept-based, ANN=neural network, Brait=vehicle, Rnd=random
We can see that some animats, like the ANN, do not even have the opportunity of tasting food or rain. The survival depends very much on luck: if a proper stimulus is generated near them, and if other animats are not around so that they can satisfy themselves. Yet the chances of obtaining necessary resources are too low, and therefore, eventually, all animats die. In this presentation, the behaviour-based animat survived for a longer time. This and the rule-based animat tend to survive more than the others in this setup, because they can move faster than the “wheeled” animats with their direct behaviours, and the concept-based animats do not even have time to learn what is edible and what is not. The random animats really do not have a chance in such a scarce environment. Also, my implementation of the behaviour-based animats resulted in reactive behaviour: the animats eat even when they are not hungry. This “bully” strategy gives the other animats a harder time than if they would all eat only when they would be hungry. I should note that this is not a property of the creatures in which the Maes’ ASM was originally implemented (Maes, 1991).
3.2. Survival in an abundant environment.
With the same initial conditions, I now set up a medium random generation ratio for the phenomena, resulting in an abundant environment. We can observe the dynamics of the internal states in Figure 8.
Even the random animat was able to drink a bit. That it randomly drank when it was under the rain was just a coincidence. However, this allows it to survive a bit more. The KEBA animat is able to learn that food is edible, but the environment is too complex, and it sadly died learning how to avoid obstacles. Still, we can see that the other animats perform quite well, and we can see that they return to their initial internal states several times. Not that they will never die (if the environment is filled with rocks, they will die), but we can see that they have a good performance. The Braitenberg animat has more trouble finding phenomena before the others, because it moves slower since it models wheels. But the neural network animats as well, and they perform better. Of course there is a chance element, but Braitenberg animats cannot keep approaching a food source or a rain source as persistently as the neural network animats.
3.3. Individual survival in environment of fixed resources.
For this experiment, I set each animat individually in an environment with five randomly generated rocks and five randomly generated food sources. There is no random generation of phenomena. Figure 9 shows the history of the internal states.
The random animat is even able to eat some food by chance. All other animats
extinguished the food sources before dying. The KEBA animat is able to learn to eat food, but
it does this reactively, so as the Maes animat, it extinguished the food sources faster than the
other animats, thus dying faster
![]() . The KEBA animat survives less time than the Maes animat
because the first one needs to learn what not to eat or drink, whereas this is “innate” in the
second. In this setup the Braitenberg animat performed better than the neural network,
precisely because it cannot keep approaching to food sources as persistently as the neural
network does, and this makes it not to exhaust the resources so fast. The rule-based animat
performed better than the wheeled animats. This is because the rules determine that it should
eat only when the internal needs are higher than 0.1, and the wheeled animats eat “on the go”
if their internal needs are higher than zero. I made another trial patching the Braitenberg
animat to eat only when its hunger is greater than 0.1, and it survived for more than fifty
thousand time steps, at the same level of the rule-based animat. But this patch causes some
inconveniences: for example, if the Braitenberg animat has less than 0.1 hunger, it will not eat,
but anyway it will do approach food persistently in a not so smart way. These inconveniences
could be patched with a threshold.
. The KEBA animat survives less time than the Maes animat
because the first one needs to learn what not to eat or drink, whereas this is “innate” in the
second. In this setup the Braitenberg animat performed better than the neural network,
precisely because it cannot keep approaching to food sources as persistently as the neural
network does, and this makes it not to exhaust the resources so fast. The rule-based animat
performed better than the wheeled animats. This is because the rules determine that it should
eat only when the internal needs are higher than 0.1, and the wheeled animats eat “on the go”
if their internal needs are higher than zero. I made another trial patching the Braitenberg
animat to eat only when its hunger is greater than 0.1, and it survived for more than fifty
thousand time steps, at the same level of the rule-based animat. But this patch causes some
inconveniences: for example, if the Braitenberg animat has less than 0.1 hunger, it will not eat,
but anyway it will do approach food persistently in a not so smart way. These inconveniences
could be patched with a threshold.
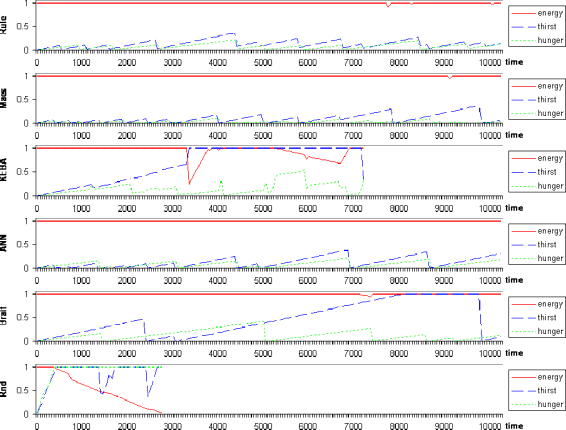 Figure 8. Survival of some animats in an abundant environment.
Figure 8. Survival of some animats in an abundant environment.
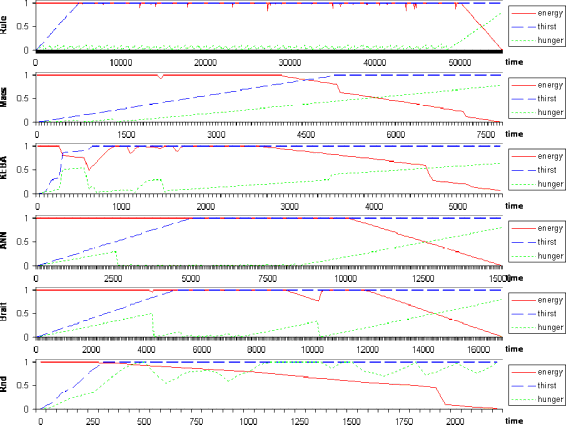 Figure 9. Survival of animats in a limited resources scenario.
Figure 9. Survival of animats in a limited resources scenario.
3.4. Discrimination of stimulus value
All the previous experiments could be argued that were easy to solve because they had very strong statistical correlations (Thornton, 2000), what Clark and Thornton (1997) have called “type one” problems. Even if they are very simple, the animats should be able to solve simple “type two” problems, where the task is more relational than statistical, and many algorithms fail to reach a solution.
One very simple relational problem is to observe if the animats are able to distinguish between food sources “larger than” others, when they are at the same distance of the animats, independently of their order, position, or absolute size. An example of this setup can be appreciated in Figure 10a.
All the animats are able to pass this test without problems. The only thing is that it does not relate much to their “cognitive” architectures, but more with the fact that they are situated in their environment. Actually, the problem is solved by interactions of the motor and perceptual systems with the environment.
Rule-based, behaviour-based, and concept-based animats solve this problem because their behaviour “approach food” simply approaches the closest food they perceive. The distance to a phenomenon is measured from the border of the animat to the border of the phenomenon. Since larger foods have larger radiuses, the measured distance to the animats will be lesser than the one of small foods, even if their centres are at the same distances from the animats. Therefore, because of this relationship with the environment, the animats will always distinguish the larger food, even when this was never programmed directly.
With the neural and Braitenberg animats the task is solved by their sensors, which basically become more active to larger stimuli, so that they approach to these without hesitation. An example of the locomotion pattern of a neural animat solving this task can be appreciated in Figure 10b.
b) Task solved by an ANN animat.
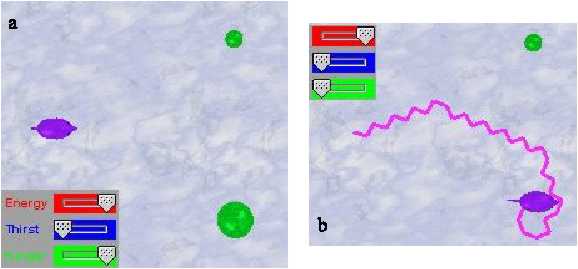 Figure 10. Discrimination of the value of different stimuli. a) Initial state.
Figure 10. Discrimination of the value of different stimuli. a) Initial state.
The fact that these tasks are solved not by the “cognitive” architectures we are comparing but rather by the interaction of the perceptual and motor systems with the environment, just reminds us of the importance of embodiment and situatedness while modelling cognition (Varela, Thompson, and Rosch, 1991; Clark, 1997; Riegler, in press).
The popular allegory of Buridan’s ass (actually in the original work of Jean Buridian it was a dog, but anyway) tells the following: the animal has to choose between two equal amounts of food. The conclusion was that it should choose at random. Otherwise, he would starve to death. In the virtual environment, we can set up a Buridian’s animat with the same amount of thirst and the same amount of hunger, and at the same but opposite distances from food and water. This problem can be seen as how to solve conflicting goals and/or motivations.
In order to test how the different animats performed in such a situation, I set them with maximum hunger and thirst, at the same distance from food and rain, but with an obstacle on the way there. Figure 11 shows the initial setup and the trails which each animat followed, together with their internal variables.
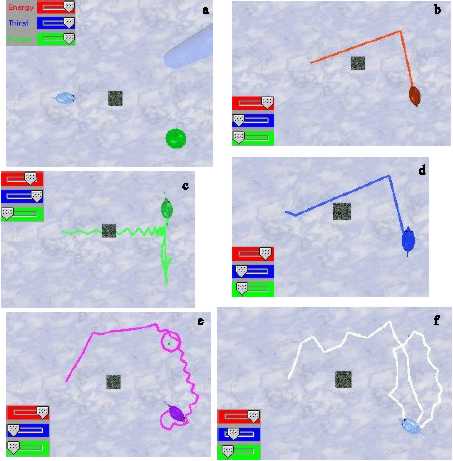 Figure 11. Buridan’s animat experiment. a) Initial setup of all animats. b) Rule-based animat. c)
Behaviour-based animat. d) concept-based animat. e) neural net animat. f) Braitenberg animat.
Figure 11. Buridan’s animat experiment. a) Initial setup of all animats. b) Rule-based animat. c)
Behaviour-based animat. d) concept-based animat. e) neural net animat. f) Braitenberg animat.
We can observe that the rule-based animats solve this situation without difficulties, giving a preference to rain over food (this is convenient since rains last only fifty time steps). Well, I designed the rules so that the animat solves this problem efficiently. My Maes animat unfortunately turned out to be Buridan’s animat... it would indeed die in the indecision if the rain would be there forever. Not to mention that the high internal needs surpassed the avoidance of the obstacle. Once the rain is transformed, the animat goes for food. The problem here was that the behaviour nodes for water and food give the same importance to thirst and hunger. I could patch this situation giving more weight to thirst, or by introducing conflicter links between these consummatory behaviour nodes. I should note again that this is a problem particular of my implementation, since the original Maes’ creatures did not suffer from this deficience. The KEBA animat, after several repetitions of the same environment, is able to learn most of the concepts required for a successful run: the only thing is that it bumped into the obstacle and lost a bit of energy, but apart from that its behavioural sequence is similar to the one of the rule-based animat. The neural animat has no problems with the indecisions, and successfully drinks and eats “on the run”, without switching. This is not so of the Braitenberg animat, which indeed switches between phenomena, and is unable to satisfy its thirst completely. The neural animats turned out to be more persistent than the Braitenberg ones, but these issues could be tuned up. Actually, the wheeled robots do not give preference of rain over food, but they give preference to the phenomena on their left side. This is because the right motor is computed first, making the animats closer to the phenomena on the left. Overinterpreting the situation, I could call this “animat preference lateralization”, as a ridiculous attempt to save the appearances. Again, the wheeled robots seem slower because of their locomotion patterns. In real robots this can easily be overcome with faster motors.
One surprising thing was that the wheeled robots could decide where to go without indecisions, even when this was not contemplated when they were designed.
I take my virtual laboratory and the experiments performed in it as a philosophical aid for discussing the suitability and equivalence of models. I do not take my simulations as a proof of my ideas, but as “opaque thought experiments” (Di Paolo, Noble, and Bullock, 2000).
With the ideas generated so far, I try to broaden the notion of cognition in order to propose one valid in as many contexts as possible. Finally I propose a simple classification of different types of cognition.
From the few experiments I presented, we can see that there is no general “best” architecture for the simple task of surviving in the presented virtual environment. We can say that each animat is better in different situations. But it seems that this is more a consequence of the particular implementation than of the paradigm on which it stands, because the models can be adjusted and refined to any desired degree of detail. In order to judge which architecture is better, we need to refer to a particular context. Their performance cannot be generally measured, but only relatively to specific tasks. We cannot say that one animat is cognitive because it uses rules and another is not because it has only direct connections. The cognition of a system is independent of its implementation. Thus, we have to observe their cognition basing ourselves on their performance.
Some models were very easy to implement in software code (rule-based, Braitenberg), others not so much (KEBA, Maes), but occasionally it is a different story if we want to implement an architecture in a real robot. Moreover, if a model works in a simulation and/or robot, it does not mean that animals function in the same way. Some models are very robust (Braitenberg), others would break up quite easily (rule-based). Some models are quite good if we have just practical purposes (rule-based), if we want things only to work, and this also depends on the experience of the engineer. But if we are interested in using them as explanatory models, the simplicity of their implementation might be secondary (KEBA). Also, if we would like to increment the systems, for example to include more environmental stimuli and internal variables, some would need to be redesigned (rule-based), others could be easily extended (Maes, KEBA). Also some models would have more ease in adapting to changes of their environment (KEBA, neural network) than others (rule-based, Braitenberg), but this does not mean that we cannot adjust different architectures in order to obtain the desired behaviour.
The animats could be criticized by saying that they are specific to their environment, and that if we take them out of their toy world, they would not exhibit cognition at all. Well, if we change the environment of any cognitive system too much, it will break (in the Ashby’s (1947) sense) inevitably (raise the temperature few thousand degrees, remove oxygen, or just leave a man in the middle of the ocean, and tell him “adapt! Don’t you know how?”). This seems to be a matter of adaptability rather than about cognition (but of course adaptability is tightly related to cognition). Yes, they are specific to their environment, but any cognitive system is.
There are dozens of other models which could be implemented in order to try to solve this or other problem. For example, we have developed a complex behaviour production system which exhibits many properties of animal behaviour desired in such a model (González, 2000; Gershenson, 2001), but it is not as easy to implement as any of the models I implemented here. We could use a huge nice set of differential equations, or GasNets (Husbands et al., 1998), or random boolean networks (Kauffman, 1969; Gershenson, 2002c), or an extension of the quantum formalism (Aerts 2002), just to name some alternatives. Moreover, we can say that different models, architectures, and paradigms, can be studying different aspects of cognition (Gershenson, 2002b). Will we find ever a “best” model? Well, as I said, it depends on our purposes and our context.
4.2. Equivalence of different models
“If you are perverse enough, you can describe anything as anything else”
—Inman Harvey
Different models of the same phenomenon have this phenomenon in common, but this simple fact does not make the models equivalent. They would be equivalent if they could produce the same results/prediction/behaviour in the same situations. They would be equivalent to a certain degree if they only produce some of this similar performance. What I said for relationships between models can also be said for the relationships between model and modelled. It is clear that we will not reach complete equivalence, because the differences between models or between model and modelled would have to disappear (the best model of a cat is the same cat (Rosenblueth and Wiener, 1945), the best model of a model is the same model). So actually we can only speak about equivalence to a certain degree.
But we can already say that all the models presented here are equivalent to a certain degree, because in most cases the animats eat when they are hungry, drink when they are thirsty and so on. The question is, how high can this degree of equivalence go?
Let us begin with a mental exercise. Since the models were programmed in a computer,
in theory they can be mapped into a Universal Turing Machine(UTM) (Turing, 1936), well,
basically because they are computable, and Turing used his machine precisely to define
computability
![]() . Therefore there is a function which would map the models to a UTM. Could
we find an inverse function, such that, any model already in the UTM, could be mapped back
to any other model? The idea is tempting, but it is not as easy as that, because basically the
model to be mapped to would need to have the capabilities of the UTM
. Therefore there is a function which would map the models to a UTM. Could
we find an inverse function, such that, any model already in the UTM, could be mapped back
to any other model? The idea is tempting, but it is not as easy as that, because basically the
model to be mapped to would need to have the capabilities of the UTM
![]() (which in theory it
has because it can be implemented in a UTM, but we would like the capabilities as a property
of the model, not of its implementation).
(which in theory it
has because it can be implemented in a UTM, but we would like the capabilities as a property
of the model, not of its implementation).
Well, let us see an example. Neural networks are mathematical models. Russell and Whitehead (1910-13) showed that all mathematics can be described in terms of logic. Therefore we can describe any neural network in terms of logic rules. Of course implementing them that way is not practical. But in this context we can certainly say that neural networks could be seen as rule-based systems. But also neural networks can be designed to produce rules (e.g. Balkenius and Gärdenfors, 1991; Gärdenfors, 1994). Actually the neural network animat can be said to be modelling the rules of the rule-based animat, but also vice versa! And, at least for my particular setup, we could say this for all the animats. We can see any animat as being a model of any other. If we want it to mimic the behaviour of other model more tightly, we just need to adjust the implementation, but in theory, there is no task that an architecture can do and another cannot do with proper extensions and patches. Then, we can say that in theory all the implemented architectures can be equivalent to any desired degree of detail.
Any implemented model could then be described in terms on another paradigm, and therefore there is nothing a paradigm can describe which another one cannot. Of course, there are different aspects of cognition modelled with less effort and in a more natural way from different perspectives. That is why we should not reject other paradigms, because we can see that different paradigms describe with more ease different aspects of cognition.
This is all nice in theory, but what about in practice? Well, it seems that it would be not so easy to implement a medical expert system for an intensive care unit using only neural networks, nor it would be easy to perform character recognition implementing only rules. Because then, in theory, any paradigm could also simulate human cognition with any degree of detail, but none has been even near. It seems that we are falling into a problem if we do not stop and identify the differences between the models and the modelled.
“Explanations are for ourselves, not for the explained”
We can make a more general distinction between models and the modelled with the ontological notion of relative being and absolute being (Gershenson, 2002a). The absolute being (a-being) is the being which is independent from the observer, and is for and in the whole universe. Therefore, it is unlimited and uncomprehensible, although we can approximate it as much as we want to. The relative being (re-being) is the being which is for ourselves, and it is different for each cognizer, and therefore dependent from the observer. It is relative because it depends on the context where each cognizer is. This context is different for all cognizers, and even the context of a cognizer can be changing constantly, with his or her notions of what re-is. It is limited because cognizers have limits.
Everything re-is a generalization of what a-is. This is because things a-have an infinitude number of properties, but can re-have only a finitude of them, no matter how huge. Therefore, we need to ignore most of these properties (e.g. the spins of the electrons of a table), making a generalization of what things a-are. However, it seems that most of the properties contemplated by different cognizers are the most relevant for their contexts, and there is not much inconvenience in ignoring many properties. But we need to be aware that we will never have a complete description of what things a-are, because it would have to be infinite and unlimited.
Different re-beings can generalize an a-being different properties, which might overlap or not. They can also make this generalization observing at different abstraction levels (Gershenson, 2002a). Re-beings can be seen as metaphors of an a-being. Figure 12 shows a diagram of how cognizers can only abstract limited parts of an a-being.
Returning to models, they can clearly be considered as special cases of re-beings which
try to approximate “the real thing” (a-being). All models, by definition, are simplifying. It
depends on what we are interested in modelling and how we justify our simplifications that we
can judge the suitability of a model
![]() .
.
But there is clearly no “best” model outside a context. Some could argue that better models are the ones in which prediction is both maximally accurate and minimally complex. But this is inside the context of information theory.
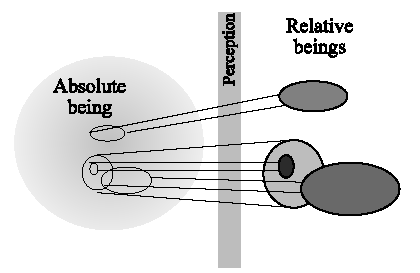 Figure 12. Relative beings as approximations of absolute being.
Figure 12. Relative beings as approximations of absolute being.
I argue that there is no way of determining which re-being is better or worse, good or bad. But one thing we can do, is to distinguish from different degrees of incompleteness. All models are incomplete, but if a model contains several models, it will be less incomplete than those models. This would be valid only in the context of <understanding|explaining>, because in a pragmatic context we would just want a model to work with the less effort. But if we try to contain as much re-beings, models, contexts, as possible, one will encounter fewer contradictions inside the less incomplete re-being, model, context.
Returning even more, to models and architectures of cognition, we can say that not only there is no general good model or architecture. And we will have a less incomplete understanding of cognition only if we study it from as many perspectives/contexts/paradigms as possible. Each model is abstracting different aspects of what cognition a-is: any cognitive behaviour can be described in terms of rules, parallel distributed processing, behaviours, mathematics, etc. And now I can say that all these models are equivalent in the degree that they model the same aspect of cognition. All my animats were modelling the same phenomenon: knowing how to survive in a simple environment. Of course some models might be easier to apply. Some might be more illuminating than others, and so on. Nevertheless, they are just different <ways of | perspectives for> describing the same thing. And this does not mean that cognition is characterized by rules, behaviours, or whatever. Things do not depend on the models we have of them.
So, what a-is cognition then?
Cognition has been studied from a variety of contexts, such as philosophy, artificial
intelligence, psychology, dynamical systems theory (Beer, 2000), etc. And it is because of this
that in each context cognition is considered with different eyes, and to be a different thing. So
in different contexts we will be able to define cognition as the manipulation of symbolic
representations (Newell, 1990), or as autopoiesis (Stewart, 1996, based on Maturana and
Varela, 1980), or as the ability to solve a problem (Heylighen, 1990), or as the ability to adapt
to changes in the environment, or as “the art of getting away with it”
![]() . We can say that
cognition re-is a different thing in different contexts, but can we say what cognition a-is? No,
but we can approach as much as we want to. The way of achieving this is to make our context
as less-incomplete as possible, by containing as many contexts as possible. Therefore, we will
not be able to dismiss a model just because it is of a certain paradigm, since all paradigms
suffer from limitedness
. We can say that
cognition re-is a different thing in different contexts, but can we say what cognition a-is? No,
but we can approach as much as we want to. The way of achieving this is to make our context
as less-incomplete as possible, by containing as many contexts as possible. Therefore, we will
not be able to dismiss a model just because it is of a certain paradigm, since all paradigms
suffer from limitedness
![]() . We can only learn from any model of cognition. We cannot say
whether a model is right or wrong outside a context. Of course, less-incomplete models will be
more robust and will be valid in more contexts. For example, we cannot judge internal
representations in a neural context just because these are not <observed|described> at that
level.
. We can only learn from any model of cognition. We cannot say
whether a model is right or wrong outside a context. Of course, less-incomplete models will be
more robust and will be valid in more contexts. For example, we cannot judge internal
representations in a neural context just because these are not <observed|described> at that
level.
I will try to reach a broader notion of cognition basing ourselves on the results and ideas exposed previously. I can make some general remarks:
• Systems can be judged to be cognitive only inside a specific context. For example, in a chess-playing context, a bee is not cognitive, but in a navigational context, it is. People agree in contexts, and these are contrasted with experience of a shared world, so we are not in danger of any radical relativism or wild subjectivism.
• Cognition is a description we give of systems, not an intrinsic constituent of them, i.e. systems do not have cognition as an element, we observe cognition from a specific context. The cognition of a system does not depend on its implementation.
• If a system performs a successful action, we can say that it knows what to do in that specific situation. This success is tied to a context and to an observer. Therefore, any system performing a successful action can be considered to be a cognitive system. This is a most general notion of cognition, and other types of cognition and definitions can be applied in different contexts with different purposes without contradicting this notion.
So, a tree knows when spring comes because it blossoms, in a specific context (not common in cognitive science, though (yet...)). And a protein knows how to become phosphorilized, and a rock knows how to fall... if we find a context where this makes sense.
It might seem that we are falling a bit into a language game. Yes, but we are victims of the same language game when we speak about human cognition! We are the ones who judge that a tree may know when to blossom, and consider this as knowledge. But this is not different from the process we make when we judge the knowledge of a human. We can describe human problem solving in terms of behaviour and classical conditioning, but we can also describe biology in terms of epistemology.
I am not insinuating that atoms and humans have the same cognitive abilities, there is a considerable difference in complexity, but not in the “essential” nature of cognition (well, the ability to do things “properly” is not entirely essential, since we judge this properness). (But for example an oxygen atom knows how to bind itself to two hydrogen atoms, and humans do not!).
We can measure this complexity
![]() , but we should note that this can only be relative to
an abstraction level (Gershenson, 2002a). And there are many definitions and measures of
complexity, so again there is no “most appropriate” measure outside a context. Moreover,
Kolen and Pollack (1994) have shown that complexity is dependent on the observer and how
she/he measures a phenomenon.
, but we should note that this can only be relative to
an abstraction level (Gershenson, 2002a). And there are many definitions and measures of
complexity, so again there is no “most appropriate” measure outside a context. Moreover,
Kolen and Pollack (1994) have shown that complexity is dependent on the observer and how
she/he measures a phenomenon.
So, what does cognitive science should study? I would suggest that cognition at all levels, not only at the human, in order to have the broadest notion of cognition. This is not just out of the hat. People already speak about bacterial (Jonker et al., 2001), immunological (Hershberg and Efroni, 2001), plant, animal(Vauclair, 1996; Bekoff, Allen, and Burghardt, 2002), machine, social, economical cognitions. What is out of the hat is proteic, molecular, atomic, planetary, etc. cognitions. Of course all of this is our interpretation, but if we take “the real thing”, what cognition a-is, we humans are not different from any other system. What changes is just how we describe ourselves (and our complexity. This complexity allows us to identify new abstraction levels, and this is very important, but at the end we all are a bunch of molecules, a mass of quarks, and infinitude of nothings...) “How does the immune system knows which antigens are foreign of the organism?” is not a question very different of “How do people know when someone is lying?”. And research in complex systems (see Bar-Yam (1997) for an introduction) has shown that systems classically considered as cognitive can be modelled with the same models of systems which are classically not considered as cognitive, and also vice versa.
That we are interpreting cognition does not mean that there is no objective notion of cognition. What it means is that it is everywhere, and therefore there is no general way (outside a specific context) to draw a borderline between “cognition” and “non-cognition”.
How useful is to describe the behaviour of a particle in terms of cognition, when physics already describes it with a different terminology? It is not about usefulness. We should just realize that cognition, in essence, a-is the same for all systems, since it depends on its description. What makes us different is just the complexity degree and the names we use to describe our cognition.
4.5. Different types of cognition
We can quickly begin to identify different types of cognition, and this will relate the ideas just presented with previous approaches for studying cognition. Of course this does not attempt to be a complete or final categorization, but it should help in understanding my ideas.
We can say that classical cognitive science studies human cognition. But of course many disciplines are involved in the study of human cognition, such as neuroscience, psychology, philosophy, etc. Human cognition can be seen as a subset of animal cognition, which has been studied by ethologists (e.g. McFarland, 1981) and behaviour-based roboticists (e.g. Brooks, 1986). But we can also consider the process of life as determined by cognition and vice versa, as the idea of autopoiesis proposes (Maturana and Varela, 1980; 1987; Stewart, 1996), in which we would be speaking about cognition of living organisms. Here we would run into the debate of what is considered to be alive, but in any case we can say that biology has studied this type of cognition. Artificial cognition would be the one exhibited by systems built by us. These can be built as models of the cognition of the living, such as an expert system, an octapod robot, or my virtual animats. But we can also build artificial systems without inspiration from biology which can be considered as cognitive (the thermostat knows when it is too hot or too cold). Most of these types of cognition can be considered as adaptive cognition, since all living organisms also adapt to modest changes in their environment, but also many artificial and non-living systems. Cybernetics (Wiener, 1948), and more recently certain branches of artificial intelligence and artificial life (e.g. Holland, 1992) have studied adaptive systems. We can contain all the previous types of cognition under systemic cognition. complex systems (Bar-Yam, 1997), and general systems theory (Turchin, 1977) can be said to have studied this type of cognition. I cannot think of a more general type of cognition because something needs to exhibit this cognition, and that something can always be seen as a system. We can see a graphical representation of these types of cognition in Figure 13.
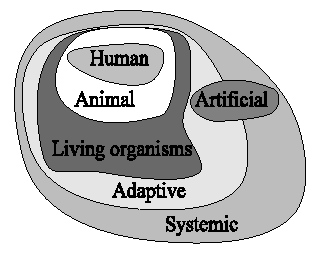 Figure 13. Different types of cognition.
Figure 13. Different types of cognition.
It is curious that cognitions which are considered to be simpler contain the ones considered to be more complex. It seems that it is that when we speak for example about human cognition, we do not see humans as a system, and when we speak for example about cognition in living organisms, we do not think right away about human cognition. We should also note that all types of cognition can be studied at different levels and from different approaches.
This is only one way of categorizing different types of cognition, but there can be several others. One could be by measuring the statistical correlations between the “inputs” and the “outputs” of a cognitive system (if we can identify them). If the outputs can be obtained by pure statistical correlations, then the cognition is simpler than if it requires complex transformation or re-representation of the inputs (Clark and Thornton, 1997; Thornton, 2000). The more transformation the inputs require, the higher and complex the cognition would be. So for example a rock would have low cognition, because if it is on the ground (input), it will stay there (output), and if it is on the air (input), it will fall (output). Now try to do the same predictions/descriptions with a cat, and we can see that they have higher cognition. This categorization is also not universal, but it seems to be useful in several contexts, rather than in a single one.
We could also identify different levels of cognition, similar to the observed levels of behaviour proposed (Gershenson, 2001; 2002b).
In classical cognitive science, it seems that there was the common belief that human cognition was a symbol system (Newell, 1990). I believe that the confusion was the following: human cognition can be modelled by symbol systems (at a certain level), but this does not mean that human cognition (absolutely) is a symbol system. But the same applies to all models. Human cognition (absolutely) is not a parallel distributed processor, nor any other model about which we can think. Things do not depend on the models we have of them. That some aspects of cognition (e.g. navigation) are implemented more easily under a certain paradigm, does not mean that natural cognitive systems do it the same way.
The implemented animats are cognitive at the same degree, because they model the same aspect of cognition roughly with the same success. Systems are not cognitive because they implement a specific architecture. Of course different architectures can be more parsimonious, others more explanatory, others easier to implement, etc.; but this is dependent of the context in which we are modelling.
Different cognitive models and paradigms can be said to be modelling different aspects of cognition. They are different metaphors, with different goals and from different contexts. Therefore, we will have a less-incomplete view of cognition if we take into account as many paradigms as possible.
There have been several proposed definitions of cognition, in different contexts. I proposed a notion which is applicable to all of these contexts and possibly more (although this makes it less practical).
A human doing the same things the animats do would be considered cognitive, just because her/his behaviour would be described with different terminology. But if the observed processes are the same, I believe that there is no intrinsic cognitive difference related to a specific task between two different systems if they solve the same task in the same context with the same success. This is why I say that cognition is observed. Just as a brain needs a body and an environment (Clark, 1997), a cognitive system also needs an observer.
Someone could say that “real” cognition is given when a system (such as a mature human) is able to explain and understand, and that we are the ones describing other systems, thus giving the cognition. I would agree, but even go further: we are the ones describing our own cognition, along with that of any cognitive system. Our cognition does not depend only on our nature, but also on how we <observe|describe> it.
Aerts, D. (2002). Being and change: foundations of a realistic operational formalism, in Aerts, D, M. Czachor, and T. Durt (eds.) Probing the Structure of Quantum Mechanics: Nonlinearity, Nonlocality, Probability and Axiomatics. World Scientific.
Ashby, W. R. (1947). The Nervous System as a Physical Machine: With Special Reference to the Origin of Adaptive Behavior. Mind 56 (221), pp. 44-59.
Arbib, M. A. (1995). The Handbook of Brain Theory and Neural Networks. MIT Press.
Balkenius, C. and P. Gärdenfors (1991). Nonmonotonic Inferences in Neural Networks. In Allen, J. A. et al. (eds.) Principles of Knowledge Representation and Reasoning: Proceedings of the Second International Conference, pp. 32-39. Morgan Kaufmann.
Balkenius, C., J. Zlatev, C. Brezeal, K. Dautenhahn and H. Kozima (2001). (Eds.) Proceedings of the First International Workshop on Epigenetic Robotics: Modeling Cognitive Development in Robotic Systems. Lund University Cognitive Studies, vol. 85, Lund, Sweden.
Bar-Yam, Y. (1997). Dynamics of Complex Systems. Addison-Wesley.
Bekoff, M., C. Allen, and G. M. Burghardt (eds.) (2002). The Cognitive Animal : Empirical and Theoretical Perspectives on Animal Cognition. MIT Press.
Beer, R. D. (1996). Toward the evolution of dynamical neural networks for minimally cognitive behavior. In Maes, P., et. al. (Eds.), From animals to animats 4: Proceedings of the Fourth International Conference on Simulation of Adaptive Behavior pp. 421-429. MIT Press.
Beer, R. D. (2000). Dynamical Approaches in Cognitive Science. Trends in Cognitive Neuroscience, 4 (3), pp. 91-99.
Berlekamp, E. R., J. H. Conway, and R. K. Guy (1982) What Is Life. Ch. 25 in Winning Ways for Your Mathematical Plays, Vol. 2: Games in Particular. Academic Press.
Braitenberg, V. (1984). Vehicles: Experiments in Synthetic Psychology. MIT Press.
Brooks, R. A. (1986). A robust layered control system for a mobile robot. IEEE Journal of Robotics and Automation. RA-2, April, pp. 14-23.
Brooks, R. A. (1991). Intelligence Without Reason. In Proceedings of the 12th International Joint Conference on Artificial Intelligence. Morgan Kauffman.
Clark, A. (1997). Being There: Putting Brain, Body And World Together Again. MIT Press.
Clark, A. and C. Thornton (1997) Trading Spaces: Computation, Representation and the Limits of Uninformed Learning. Behavioral and Brain Sciences, 20, pp. 57-90.
Clark, A. and J. Toribio (1995). Doing Without Representing? Synthese 101, pp. 401-431.
Di Paolo, E. A., J. Noble, and S. Bullock (2000). Simulation Models as Opaque Thought Experiments. Artificial Life VII, pp. 1-6.
Fodor, J. A. (1976). The Language of Thought. Harvard University Press.
Fodor, J. A. and Z. W. Pylyshyn (1988). Connectionism and Cognitive Architecture: A Critical Analysis. In Pinker, S. and J. Mehler (Eds.). Connections and Symbols. MIT Press.
Gärdenfors, P. (1994). How Logic Emerges from the Dynamics of Information. In van Eijck, J. and A. Visser, Logic and Information Flow, pp. 49-77. MIT Press.
Gärdenfors, P. (2000). Conceptual Spaces. MIT Press.
Gershenson, C. (1998). Lógica multidimensional: un modelo de lógica paraconsistente. Memorias XI Congreso Nacional ANIEI, pp. 132-141. Xalapa, México.
Gershenson, C. (1999). Modelling Emotions with Multidimensional Logic. Proceedings of the 18th International Conference of the North American Fuzzy Information Processing Society (NAFIPS ‘99), pp. 42-46. New York City, NY.
Gershenson, C. (2001). Artificial Societies of Intelligent Agents. Unpublished BEng Thesis. Fundación Arturo Rosenblueth, México.
Gershenson, C. (2002a). Complex Philosophy. Proceedings of the 1st Biennial Seminar on Philosophical, Methodological & Epistemological Implications of Complexity Theory. La Habana, Cuba.
Gershenson, C. (2002b). Behaviour-based Knowledge Systems: An epigenetic path from Behaviour to Knowledge. To appear in Proceedings of the 2nd Workshop on Epigenetic Robotics. Edinburgh.
Gershenson, C. (2002c). Classification of Random Boolean Networks. To appear in Artificial Life VIII. Sydney, Australia.
Gershenson, C. (unpublished). Adaptive Development of Koncepts in Virtual Animats: Insights into the Development of Knowledge. Adaptive Systems Project, COGS, University of Sussex, 2002.
Gershenson, C. and P. P. González, (2000). Dynamic Adjustment of the Motivation Degree in an Action Selection Mechanism. Proceedings of ISA '2000. Wollongong, Australia.
Gershenson, C., P. P. González, and J. Negrete (2000). Thinking Adaptive: Towards a Behaviours Virtual Laboratory. In Meyer, J. A. et. al. (Eds.), SAB2000 Proceedings Supplement. Paris, France. ISAB Press.
González, P. P. (2000). Redes de Conductas Internas como Nodos-Pizarrón: Selección de Acciones y Aprendizaje en un Robot Reactivo. PhD. Dissertation, Instituto de Investigaciones Biomédicas/UNAM, México.
González, P. P., J. Negrete, A. J. Barreiro, and C. Gershenson (2000). A Model for Combination of External and Internal Stimuli in the Action Selection of an Autonomous Agent. In Cairó, O. et. al. MICAI 2000: Advances in Artificial Intelligence, Lecture Notes in Artificial Intelligence 1793, pp. 621-633, Springer-Verlag.
Hallam, B., D. Floreano, J. Hallam, G. Hayes, and J.-A. Meyer (2002) (eds.). From Animals to Animats 7: Proceedings of the Seventh International Conference on Simulation of Adaptive Behavior. MIT Press.
Hershberg, U. and S. Efroni (2001). The immune system and other cognitive systems. Complexity 6 (5), pp. 14-21.
Heylighen F. (1990) Autonomy and Cognition as the Maintenance and Processing of Distinctions, In: Heylighen F., Rosseel E. & Demeyere F. (eds.), Self-Steering and Cognition in Complex Systems. Gordon and Breach, pp. 89-106.
Holland, J. (1992). Adaptation in Natural and Artificial Systems. 2nd Ed. MIT Press.
Husbands, P., T. Smith, N. Jakobi, and M. O'Shea (1998). Better Living Through Chemistry: Evolving GasNets for Robot Control, Connection Science, 10(4), pp. 185-210.
Jakobi, N., P. Husbands, and I. Harvey (1995). Noise and the reality gap: The use of simulation in evolutionary robotics. In Advances in Artificial Life: Proceedings of the 3rd European Conference on Artificial Life, pp. 704-720. Springer-Verlag, Lecture Notes in Artificial Intelligence 929.
Jonker, C. M., J. L. Snoep, J. Treur, H. V. Westerhoff, and W. C. A. Wijngaards. (2001). Embodied Intentional Dynamics of Bacterial Behaviour. In: Pfeifer, R. and M. Lungarella (eds.), Proceedings of the International Workshop on Emergence and Development of Embodied Cognition.
Kauffman, S. A. (1969) Metabolic Stability and Epigenesis in Randomly Constructed Genetic Nets. Journal of Theoretical Biology, 22, pp. 437-467.
Kirsch, D. (1991). Today the earwig, tomorrow man? Artificial Intelligence 47, pp 161-184.
Kolen, J. F. and J. B. Pollack (1995). The Observer’s Paradox: Apparent Computational Complexity in Physical Systems. Journal of Experimental and Theoretical Artificial Intelligence, 7, pp. 253-277.
Lambrinos, D. and Ch. Scheier (1995). Extended Braitenberg Architectures. Technical Report AI Lab no. 95.10, Computer Science Department, University of Zurich.
Lenat, D. and E. Feigenbaum (1992). On the Thresholds of Knowledge. In Kirsh, D. (ed.) Foundations of Artificial Intelligence. MIT Press.
Maes, P. (1990). Situated agents can have goals. Journal of Robotics and Autonomous Systems, 6 (1&2).
Maes, P. (1991). A bottom-up mechanism for behaviour selection in an artificial creature. In J. A. Meyer and S.W. Wilson (eds.), From Animals to Animats: Proceedings of the First International Conference on Simulation of Adaptive Behaviour. MIT Press/Bradford Books.
Maes, P. (1994). Modelling Adaptive Autonomous Agents. Journal of Artificial Life, 1 (1-2), MIT Press.
McClelland, J. L., D. E. Rumelhart and the PDP Research Group (Eds.) (1986). Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 2: Psychological and Biological Models. MIT Press.
McFarland, D. (1981). The Oxford Companion to Animal Behavior. Oxford University Press.
Maturana, H. R. and F. J. Varela (1980). Autopoiesis and Cognition: The Realization of the Living. Reidel.
Maturana, H. R. and F. J. Varela (1987). The Tree of Knowledge: The Biological Roots of Human Understanding. Shambhala.
Newell, A. (1980). Physical Symbol Systems. Cognitive Science 4, pp. 135-183.
Newell, A. (1990). Unified Theories of Cognition. Harvard University Press.
Newell, A. and H. Simon (1972). Human Problem Solving. Prentice-Hall.
Peirce, C. S. (1932). Collected Papers of Charles Sanders Peirce, vol. 2: Elements of Logic. Hartshore, C. and P. Weiss (eds.). Harvard University Press.
Piaget J. (1968). Genetic Epistemology. Columbia University Press.
Pylyshyn, Z. W. (1984). Computation and Cognition. MIT Press.
Riegler, A. (in press). When Is a Cognitive System Embodied? To appear in: Cognitive Systems Research, special issue on “Situated and Embodied Cognition”.
Rosenblueth, A. and N. Wiener (1945). The role of models in science. Philosophy of Science, 12, pp. 316-321.
Rumelhart, D. E., J. L. McClelland, and the PDP Research Group (Eds.) (1986). Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1: Foundations. MIT Press.
Russell, B. and A. N. Whitehead (1910-13). Principia Mathematica. Cambridge University Press.
Seth, A. K. (1998). Evolving Action Selection and Selective Attention Without Actions, Attention, or Selection. In Pfeifer, R., et. al. (Eds.), From animals to animats 5: Proceedings of the Fifth International Conference on Simulation of Adaptive Behavior, pp. 139-147. MIT Press.
Shortliffe, E. (1976). Computer Based Medical Consultations: MYCIN. Elsevier.
Slocum, A. C., D. C. Downey, and R. D. Beer (2000). Further experiments in the evolution of minimally cognitive behavior: From perceiving affordances to selective attention. In Meyer, J.-A., et. al. (Eds.), From Animals to Animats 6: Proceedings of the Sixth International Conference on Simulation of Adaptive Behavior, pp. 430-439. MIT Press.
Smolensky, P. (1988). On the Proper Treatment of Connectionism. Behavioural and Brain Sciences 11, pp. 1-23.
Stewart, J. (1996). Cognition = life: Implications for higher-level cognition. Behavioural Processes 35, (1-3) pp. 311-326.
Thornton, C. (2000). Truth From Trash: How Learning Makes Sense, MIT Press.
Turchin, V. (1977): The Phenomenon of Science. A cybernetic approach to human evolution. Columbia University Press.
Turing, A. M. (1936-7). On Computable Numbers, with an Application to the Entscheidungsproblem. Proc. London Math. Soc. (2), 42, pp. 230-265.
Tyrrell, T. (1993). Computational Mechanisms for Action Selection. PhD. Dissertation. University of Edinburgh.
Varela, F., E. Thompson, and E. Rosch (1991). The Embodied Mind: Cognitive Science and Human Experience. MIT Press.
Vauclair, J. (1996). Animal Cognition. Harvard University Press.
Walter, W. G. (1950). An Imitation of Life. Scientific American 182 (5), pp. 42-45.
Walter, W. G. (1951). A Machine That Learns. Scientific American 185 (2), pp. 60-63.
Webb, B. (2001). Can Robots Make Good Models of Biological Behaviour? Behavioral and Brain Sciences 26 (6).
Wiener, N. (1948). Cybernetics; or, Control and Communication in the Animal and the Machine. MIT Press.
Wolfram, S. (2002). A New Kind Of Science. Wolfram Media.
7. Appendix A: KEBA description
My model generates recursively regularities from sensory input. These sensations can include perceptual, introceptual (sensing the internal medium (e.g. hunger, thirst)), and propioceptual (sensing motor actions and body). I add noise to these signals attempting to approach inexactitudes in real environments (Jakobi, Husbands, and Harvey, 1995). The information from the sensors is mapped to the interval [0..1] and each input is taken as a concept (protoconcept) of the zero level. Each one determines a coordinate of a multidimensional vector, as defined in multidimensional logic (Gershenson, 1998; 1999), which will be considered as the coordinates of the centres of new concepts. These concepts are generated in dependence of the experiences of the animat, combining sensory inputs, and are of level one. They can create the coordinates of multidimensional vectors of concepts of level two, which can determine coordinates at a third level, and so on. The coordinates determine the centres of open balls (Gershenson, 1999), which are fuzzy neighbourhoods that along with two radiuses r1 and r2 determine the linear fuzzy membership function (1) of the Euclidean distance d (calculated with Pythagoras) of a point to the centre of the open ball.
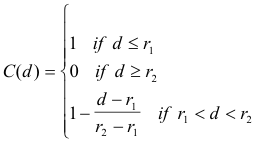 (1)
(1)
Each concept in KEBA has a value v, an activation a, and a stability s. The values of the concepts at level zero are the signals arriving from the sensors. The values of the concepts of levels n>0 are determined by how far the activations of the concepts of level n-1 are from the centre of the concept, namely C(d) (1). The activation represents the history of v’s and is determined by (2):
![]() (2)
(2)
where A is the activation potential raised to the power of the level n, and ι gives an importance to the previous experiences, acting as a persistence factor. With An, the activation of a concept will take more importance from previous values if the concept is in a higher level, and therefore will have a slower decay.
The concepts active at time t in the level n determine a multidimensional vector, which might fall into an open ball of a concept of the level n+1, altering its value as in (1), but if not they create a new concept at level n+1 with centre at the coordinates determined by the value and activation of one. If the activations of the concepts at level n do not fall into the open ball of a concept of the level n+1, the latter is updated with v=0.
The stability of the concepts represents the change of the activation. The value of s is bounded to the interval [0..1]. It is determined by (3)
![]() (3)
(3)
where κ is the speed of the stability. It does not require to be higher than the noise. If κ is small, concepts will be abstracted only when the environment is more stable. The larger the value of κ, the more details of the environment will be abstracted, reaching a maximum at κ=1.
The values of v, a, and s are updated recursively for the level n+1, creating new concepts when necessary, only when all the concepts of the level n are stable (s=1) and more than one concept of the level n is active (a>0). Concepts are “forgotten” if they have not been active after a determined period of time. There is also a maximum number of concepts and a maximum number of levels which can exist at a time. Figure 14 shows an example of a concept configuration of KEBA.
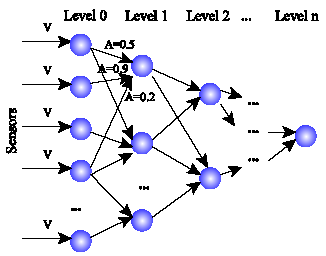 Figure 14. Example. Activations at level n determine
the values of concepts at level n+1
Figure 14. Example. Activations at level n determine
the values of concepts at level n+1
KEBA Animats sense only properties of the phenomena in the virtual environment, such as colours, odour, flavour, hardness, loudness. For each phenomena inside their radius of perception the sensors become active and are mapped into a concept of level one. So, for example, a food perceived will have a high value of green, positive odour, and if the animat is touching it, good flavour and medium hardness. Combinations of these concepts produce concepts at level two (like “food and lightning”). If there would be not distinctive properties between phenomena, or if the radiuses of concepts are too large, animats would be “confused”, having the same concept for different phenomena.
Each concept has a link to all potential actions. For deciding an action, every concept with v>0 contributes to a sum according to (4):
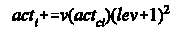 (4)
(4)
where acti is the total activation for action i, actci is the strength of the link (similar to a weight in an artificial neural network), and lev is the level in which the concept is. Therefore, concepts at higher levels will contribute more to the action selection. After the results from all the concepts have been summed, the action will be just the maximum of all acti‘s. These actions are the same behaviours that behaviour-based and rule-based animats can execute: none, explore, eat, drink, avoid, approach food, rain, and lightning. Therefore, KEBA animats simplify the motor system, but not the perceptual.
Since the animats are generated with random links, their initial performance is no better than the one of an animat executing actions randomly. But the links between concepts and actions are modified by a simple reinforcement learning scheme, depending on the satisfaction produced by the current action. For example, there is positive satisfaction if the animats eat food, and negative if they eat rocks. I could argue that these responses are designed through evolution, just as bats need to learn by experience which moths are poisonous and which are not, but they know from birth what is to taste good and to taste sour. For my animats I designed which are the reinforcement rules. The algorithm is as follows: if the executed action produces a positive satisfaction (the action was “correct”), and the maximum link of the concept is the one of the executed action, then this is boosted. If the maximum link is to a different action, then this one is decremented hyperbolically (Gershenson and González, 2000). If the satisfaction is negative, if the maximum link of the concept is towards the executed action, then the link is severely punished. If the maximum link is towards another action, then this is hyperbolically incremented (Gershenson and González, 2000).
The main idea is that through time concepts should link to actions which produce a positive satisfaction.
To illustrate KEBA a bit more, I present a small experiment.
Since KEBA animats need to learn and develop concepts in regular environments, I implemented in my virtual laboratory an option for repeating the simulation each certain number of time steps, after which the phenomena including animats are restored to their original position, except for the concepts of the KEBA animats, which develop through several iterations or trials.
Using this feature, I studied how well the KEBA animats developed varying the number of allowed concept levels. The initial setup was the following: a hungry KEBA animat perceives a food source, but there is a rock on the way to the food, so it should also avoid this. It would be easier (faster) if the animat would first learn how to eat food, then how to avoid obstacles, and then how to do both things at once, but I set this task a bit more difficult in order to compare the performance of the animats with different maximum concept levels. In Figure 15 we can appreciate the initial setup, an example of a failed trial, and an example of a successful trial. In a failed trial, the animat is not able to eat or avoid the obstacle. A successful trial is that when the rock is avoided and the food is eaten.
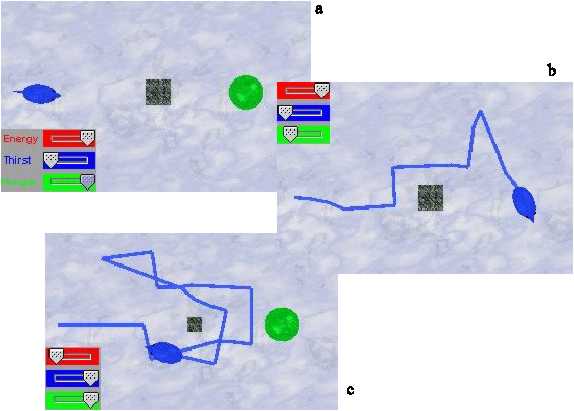 Figure 15. KEBA animat attempting to learn to avoid
obstacles while approaching food. a) Initial state for each repetition. b)
Successful trial. c) Unsuccessful trial.
Figure 15. KEBA animat attempting to learn to avoid
obstacles while approaching food. a) Initial state for each repetition. b)
Successful trial. c) Unsuccessful trial.
In Figure 16 we can observe the success of each repetition of the KEBA animat with different maximum concept levels, with a maximum number of concepts of fifty.
We can see that only one level is sufficient for associating in some cases the correct actions, but since, for example, a rock is present when the animat should be eating, but also approaching food, this makes correct associations to be lost. But if we allow several levels, since concepts of higher levels have greater importance, there is too much noise from higher concepts which represent concepts which were active in previous repetitions. Three levels are not that bad, but the best seems to be with two. The concepts are not associated permanently with actions, since they can become active in different situations which correspond in some cases to a proper action and in some others not.
 Figure 16. History of internal states of KEBA animats
after each repetition with different maximum concept levels. One repetition
equals sixty time steps.
Figure 16. History of internal states of KEBA animats
after each repetition with different maximum concept levels. One repetition
equals sixty time steps.
8. Appendix B: Virtual Laboratory Specification
The virtual laboratory, its source code, and documentation can be obtained from https://bingweb.binghamton.edu/%7Ecgershensong/unamcogs/keb.
I used Java programming language, with aid of the Java3D libraries for the creation of the virtual environment and phenomena, and the Java SWING libraries for the development of the GUIs. The programming was performed using Borland JBuilder 6.
The laboratory presented in this dissertation was based on a simpler previous version. As a rough comparison, the source code of the previous version (2.0) was 99 Kb in 16 classes and the one of the actual version (3.0) is 181 Kb in 38 classes. Version 1.0 was used for courses in the autumn term, 2.0 for courses in the spring term, and 3.0 for the dissertation. Among the work carried out exclusively for the dissertation is the following:
• Separated KEBA functions from Animat and AnimatFrame classes.
• Implemented AnimatRule, AnimatMaes, AnimatNN, AnimatBrait, and their Frame classes, where the graphical interfaces are implemented.
• Option for saving history of internal states of animats in text files, for generating graphs.
• Animats can leave trails.
• Added functions for repeating simulations each certain number of steps.
• Added more phenomena: spots of different colours (useful for tuning KEBA)
• Random generation of phenomena as a slider instead of an on/off button.
• Refinement of KEBA model.
Screenshots of the virtual laboratory window and one of the animat windows can be appreciated in Figure 17 and Figure 18, respectively.
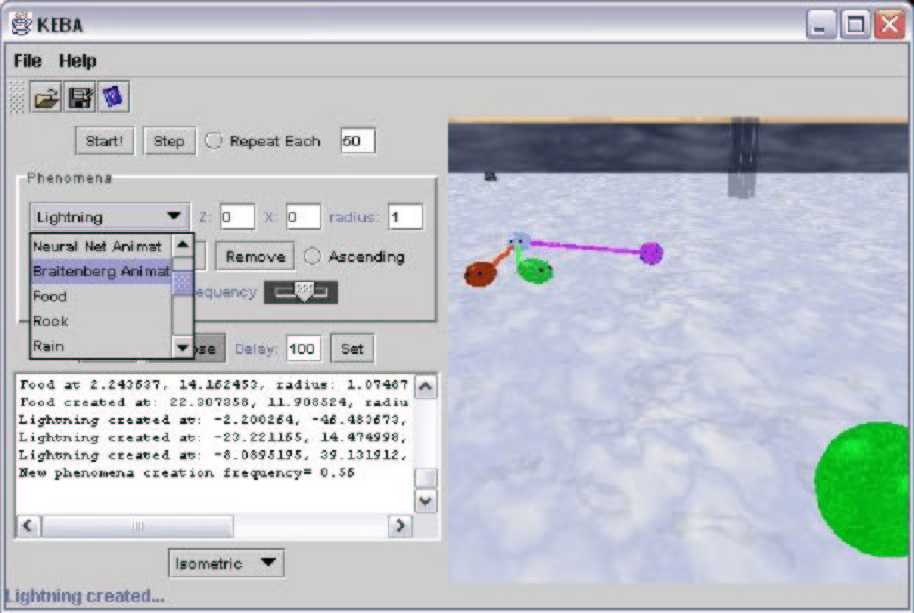 Figure 17. Screenshot of virtual laboratory main
window.
Figure 17. Screenshot of virtual laboratory main
window.
All the important classes of the virtual laboratory are in the keba package. The main class is KEBA, which is a JFrame (through inheritance), and implements the Runnable interface, in order to be able to run a thread for the simulation (and stop it). It contains the main GUI controls, as well as the VirtualUniverse, where the 3D objects are rendered into. It has a phenomena Vector, which contains the different possible objects which can be created in the VirtualUniverse. This Vector can be saved into a file, along with essential variables, and later to be loaded to restore a simulation.
 Figure 18. Screenshot of AnimatMaesFrame.
Figure 18. Screenshot of AnimatMaesFrame.
Phenomenon is an abstract class, with all the common properties of objects which will be created in the virtual world. It extends the BranchGroup class, which allows a Phenomenon to be inserted in the VirtualUniverse, and implements the Serializable interface, which allows the persistence of the objects of this class (i.e. to save and load them). The classes Food, Rock, Rain, Lightning, Spot, and Animat extend the Phenomenon class. Spots of different colours inherit the properties of the abstract Spot class: SpotBlack, SpotBlue, SpotGreen, SpotRed, SpotRnd, SpotWhite, and SpotYellow. The Animats have an AnimatFrame, to observe and control the internal variables through a GUI, and the AnimatFrame has a reference to the same Animat object, to be able to update each other’s properties. Animat and AnimatFrame contain variables and methods required by any kind of animat, such as internal states, trails, etc. These two are abstract classes, which are inherited by each animat type: AnimatBrait, AnimatKEBA, AnimatMaes, AnimatNN, and AnimatRule from Animat; and AnimatBraitFrame, AnimatKEBAFrame, AnimatMaesFrame, AnimatNNFrame, and AnimatRuleFrame from AnimatFrame. All Animat subclasses use a StatStream for saving their internal state history to text files.
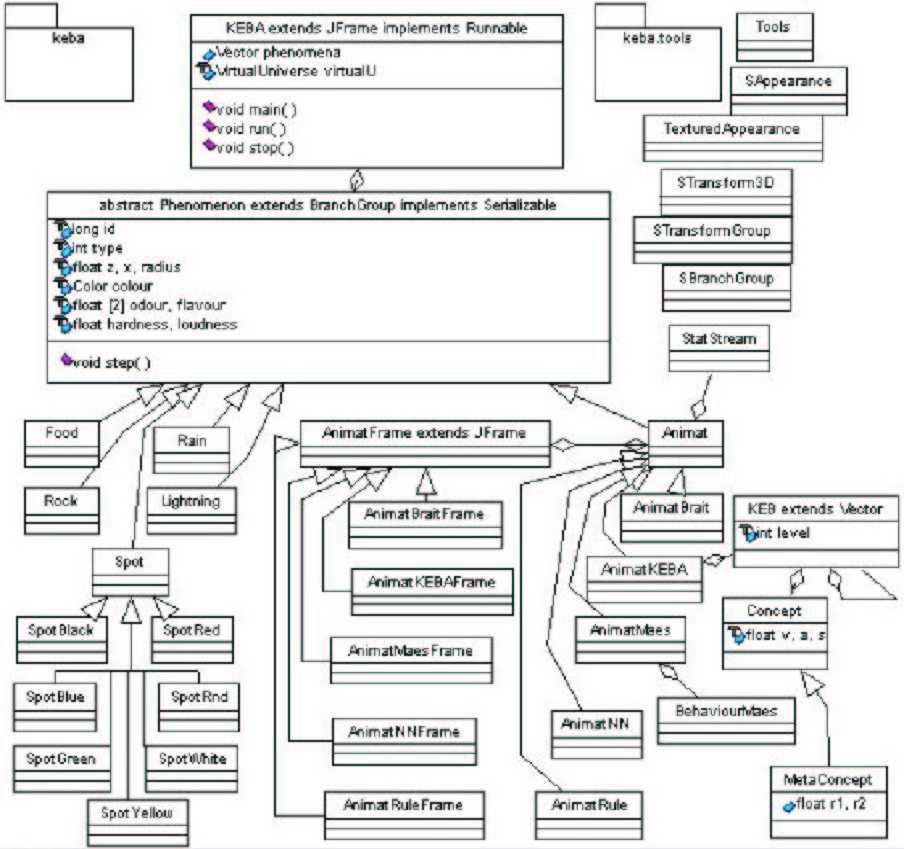 Figure 19.UML diagram showing the relationships
between classes.
Figure 19.UML diagram showing the relationships
between classes.
Each instantiated Animat has different methods implementing their particular models, motor and perceptual systems. Their respective AnimatFrame allows the monitoring and manipulation of mechanisms and variables. An AnimatMaes has an array of BehaviourMaes for implementing the network of behaviours. An AnimatKEBA also has a KEB class, which basically is a Vector of Concepts with another KEB (for the next level), and this allows to have recursively as much levels (KEBs) as the memory allows (about 70 with 192 Mb RAM). KEBs have Concepts only at level zero. The next levels have Metaconcepts, which include the methods necessary for calculating the multidimensional neighbourhoods, and to localize their parents. These three classes constitute my model for concept abstraction from perception. They were developed in a general way, such that the model can be reused in a different context with ease.
In the package keba.tools there are classes not essential to the virtual laboratory, but which are just an aid in the programming. The methods of the Tools class provide simple functions for truncating Strings. TexturedAppearances extend the Appearance class in order to automatize the loading of textures for different objects in the virtual world. StatStream, SAppearance, SBranchGroup, STransformGroup and STransform3D are just extensions of 3D classes which implement the Serializable interface, to be able to make them persistent.
A simplified UML diagram showing the relationships between the classes can be appreciated in Figure 19.

| Back to main |