"El Juego de la Vida en Tres Dimensiones"
Carlos Gershenson García
Fundación Arturo Rosenblueth
Resumen
Primero se introduce al lector con un poco de la historia del Juego de la Vida. Después se explican su consecuencias en dos dimensiones, y por último se discuten sus propiedades al llevar el Juego de la Vida a una tercera dimensión, y se muestran algunos ejemplos.
Introducción
En 1970, John Comway publicó su libro "The Game of Life". Él creó el Juego de la Vida como una forma de representar un sistema biológico. Utilizó una matriz bidimensional booleana (Es decir, una cuadrícula en la que en cada cuadro suyo sólo podía haber dos estados: verdadero y falso). Si una posición de la matriz era verdadera, esta se consideraba como una "célula", y si era falsa, como un espacio vacío. Utilizó simples reglas para el juego: si alrededor de una célula (de sus ocho vecindades) había menos de dos células, esta moría. Si tenía más de tres, también moría, al haber una sobrepoblación de células. Ahora bien, si alrededor de un cuadro vacío había tres células, en el espacio vacío nacía una nueva célula. A esto se le llamó reproducción trisómica. Al proponer estas simples reglas, no creo que se imaginara que se iban a desarrollar "organismos" tan sorprendentes como los que se desarrollaron.
El Juego de la Vida en Dos Dimensiones
A continuación se muestran algunos organismos estables de el Juego de la Vida en dos dimensiones:
Cubos y Panales:
XX X
XX X X
X X
X
Estas estructuras son estáticas. No sufren ningún cambio si no llega alguna célula a sus vecindades.
Traffic Lights (Semáforos):
XXX
Estos organismos parpadean constantemente.
Osciladores:
XXX XX XX
XXX XX XX
XXX X X
XXX X X X X
XXX X X X X
XXX XX XX
Estas estructuras pasan por varios estados para siempre regresar al mismo.
Glider (Deslizador):
X
X
XXX
Este organismo se desliza por la matriz de una forma diagonal.
Spaceship (Nave espacial):
X
X
X X
XXXX
Esta estructura se desliza horizontalmente. Hay varios tipos. Las cuatro células que hay en la base también pueden ser cinco o seis.
Eater (Comedor):
XX
X
XXX
X
Este organismo se "come" a los gliders y a las spaceships, ya que los destruye sin alterarse su estado.
Se han descubierto organismos mucho más complejos, como una "trepadora", en la cual las células parece que se desplazan hacia arriba sobre dos ejes diagonales.
Hasta se podría decir que se han desarrollado "sistemas", como un Generador de Gliders, el cual consta de cuatro organismos, que producen uno nuevo (el glider) cada cierto tiempo.
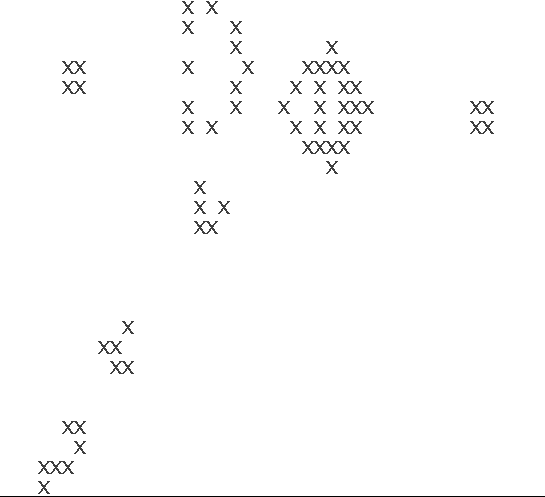
Generador de Gliders
También se puede apreciar cómo en una colonia estable de cubos, al introducir sólo una célula (un virus), se desestabiliza todo el sistema.
Virus
Al admirarme ante tal variedad de estructuras, imaginé que sería todavía más fascinante un Juego de la Vida en tres dimensiones. Desgraciada o afortunadamente ( la primera porque ya no fue novedad, la segunda porque me costó mucho menos trabajo) encontré que ya se había hecho por lo menos en un protector de pantalla de Linux. Tomé sus reglas y algunos de sus organismos y les apliqué mis conocimientos de Topología para crear mi
Juego de la Vida en Tres Dimensiones
Para poder desarrollar un Juego de la Vida en tres dimensiones primero me vi con el problema de su representación.
Me fijé un espacio de 10*10*10 cubos y representé en perspectiva el cubo que los contenía. Después hice las funciones para representar , a partir de los centros de cada cubo pequeño, con círculos las células. Estas funciones toman coordenadas cartesianas de los ejes X,Y y Z, los rotan, sacan su proyección isométrica y lo colocan en sus coordenadas respectivas en la pantalla.
Dado que el espacio de 10*10*10 es pequeño, decidí hacer un espacio cíclico. Esto es, unir las caras opuestas del cubo. Una representación topológica de un espacio cíclico, o hipertoroide se muestra a continuación.
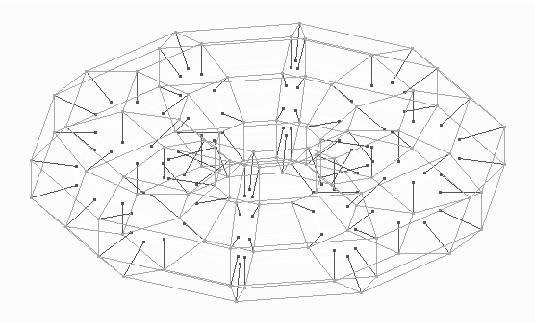Hipertoroide
Como este trabajo no está enfocado a explicar la Topología, no se explican los métodos ni la teoría para desarrollar esta figura.
El caso es que al "ciclar" el cubo, se puede ampliar mucho más la interacción entre las células. Esto se verá más adelante.
Después la cuestión es fijar las reglas. Para que nazca una célula, tiene que haber cinco células a su alrededor (reproducción pentasomática). Si alrededor de una célula hay menos de cuatro o más de cinco, muere.
El programa (LIFE3D.EXE, hecho en Turbo Pascal), para las condiciones iniciales abre un archivo de texto. En él va leyendo las casillas en las cuales hay células en un tiempo igual a cero. Para notar la profundidad, las células van cambiando de color con respecto a su coordenada en X.
Juego de la Vida en 3D
Hay varios archivos, que incluyen figuras similares a el Juego de la Vida en dos dimensiones. Hay el equivalente de las estructuras estáticas (cubos y panales), osciladores, gliders, virus, etc. Así como hay muchas más posibilidades de nuevos organismos, es mucho más difícil encontrar nuevos. Para eso se puede generar un patrón aleatorio con un porcentaje deseado, para poder encontrar estructuras nuevas.
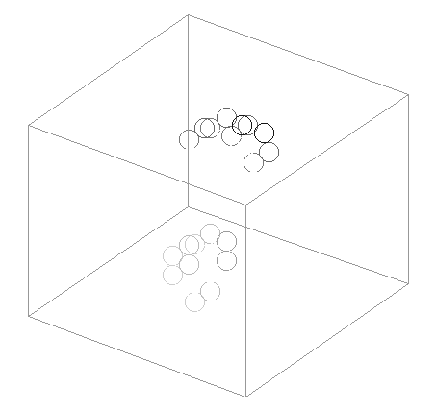Gliders
En el caso de lis gliders, por ejemplo, si uno de estos llegase a una pared normal, moriría, ya que no tendría espacio para interactuar. Esta limitación de espacio dificulta el estudio de los organismos y demanda unas matrices de dimensiones muy grandes. Para evitarnos esta contrariedad, se toman en cuenta las vecindades de la cara opuesta, así el glider puede navegar por todo el espacio una y otra vez, y puede ser observado a placer. También amplia mucho el promedio de vida de un sistema creado aleatoriamente, ya que las células interactúan mucho más. Para comprobar esto, se puede activar o desactivar el hipertoroide, y uno se da cuenta fácilmente de la diferencia. También, se puede regular la velocidad, para apreciar con más o menos detenimiento una reacción.
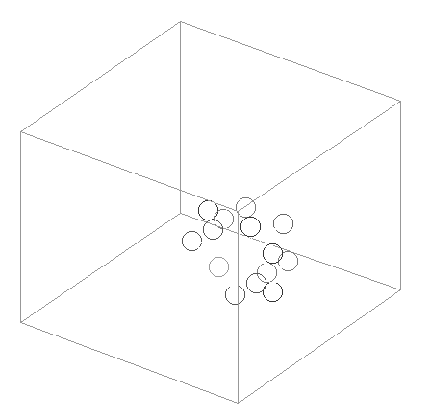Oscilador
Conclusiones
Sistemas de simulación biológica como este nos permiten comprender mucho mejor fenómenos como la evolución. Si con un sistema tan sencillo, se crean organismos tan fascinantes, con uno complicado, hasta se podrían crear simuladores de presentes alternativos. Es decir, ¿qué hubiese pasado si en la atmósfera hubiera 10% menos oxígeno? ¿Qué sucedería si la temperatura media de la tierra ascendiese cinco grados centígrados? ¿Cómo sería la vida con condiciones iniciales impuestas rigurosamente? Preguntas similares nos acechan, y buscamos por una respuesta. ¿Por curiosidad científica o porque nos gusta jugar a Dios?
Bibliografía
--Comway, John. "The Game Of Life." 1970.
--Spivak, Michael. "Cálculo en Variedades". Ed. Reverté. 1988.
