
"Aplicaciones de la Topología"
Carlos Gershenson García
Fundación Arturo Rosenblueth
Resumen
En el presente trabajo se abordan algunas aplicaciones de la Topología en la Computación, como el Juego de la Vida. Se tratan de ampliar los conocimientos actuales sobre estas aplicaciones y sus representaciones gráficas. Se apoya la exposición con un simulador de tiempo cíclico. También se hace una propuesta para definir el Universo como un tiempo cíclico.
Introducción
Si uno no tiene conocimientos de Topología o de Geometría, primero se hace una breve introducción a la Topología y se definen los términos empleados en la propuesta.
El objetivo de esta es representar y aplicar espacios y tiempos cíclicos, con ayuda de la Topología. Para esto primero se definen las líneas y planos cíclicos. Después se extienden las definiciones para dimensiones mayores y se mencionan algunas aplicaciones.
Por último se propone definir al Universo como un tiempo cíclico.
Topología
Las limitaciones que tienen las dimensiones Euclidianas llevaron a los matemáticos a crear la Topología. Esta no estudia, como la Geometría clásica, cantidades medibles, como ángulos, distancias, áreas, etc.; sino se enfoca a estudiar la continuidad y las vecindades de un punto.
Figuras como la banda de Möebius, o la botella de Klein son estudiadas por la topología, ya que la Geometría Euclidiana no puede describirlas con precisión.
En la Topología, se estudian las propiedades de espacio que no se alteran, aunque estos sean doblados, estirados o encogidos, como las vecindades de los puntos.
La Topología tiene aplicaciones desde cosmología y física de partículas hasta la estructura geométrica de proteínas.
Cubos multidimensionales
Un cubo de dimensión Euclidiana n, o n-cubo, se puede formar a partir de dos cubos paralelos de dimensión Euclidiana n-1, unidos en sus vértices por vectores ortogonales de la magnitud de una arista del cubo n-1.
Un punto tiene dimensión Euclidiana 0. Si se unen dos puntos, se obtiene una línea, de dimensión Euclidiana 1. Si se unen dos líneas por sus vértices, se obtiene un cuadrado, de dimensión Euclidiana 2. Si se unen dos cuadrados por sus vértices, se obtiene un cubo, de dimensión Euclidiana 3. Si se unen dos cubos por sus vértices, se obtiene un hipercubo, de dimensión Euclidiana 4. Si se unen dos hipercubos por sus vértices, se obtiene un cubo de 5 dimensiones, y así ad infinitum.
Una forma de identificar fácilmente la dimensión de un cubo es contar las aristas que salen de cada vértice, ya que el numero de aristas será igual a la dimensión.
Líneas y Planos Cíclicos
Si se toma un segmento de recta y se dobla, de tal forma que se unan sus extremos, se obtendrá un círculo. Este es una línea cíclica, ya que si uno recorre la línea, al llegar al final de esta, se encontrará de nuevo con el principio.
Al tomar un plano y unir sus dos extremos opuestos, se obtiene un cilindro. Si se unen los extremos del cilindro, se obtiene un toroide. Un toroide es un plano cíclico. En tres dimensiones tiene una forma de dona. Si uno, al moverse en él, llega al extremo superior y sigue subiendo, saldrá por el extremo inferior. Lo mismo para los extremos derecho e izquierdo. El toroide ya ha sido ampliamente estudiado y tiene numerosas aplicaciones. Por ejemplo, en un Juego de la Vida bidimensional, se puede aplicar un toroide para que las "células" no tengan limitaciones de espacio. O también en el clásico Pac-Man. Se sale por un lado y se regresa por el otro.
La estructura de un menú, visto como listas cíclicas, hasta cierto punto, se podría decir, que tiene las propiedades de un toroide.
Espacios y Tiempos Cíclicos
Ahora, si se toma un cubo y se le aplica el mismo método para unir sus lados opuestos, se tendrá un espacio cíclico.
El criterio para hacer cubos cíclicos es el de reducir todos los vértices del cubo, de n-dimensiones, a un sólo punto. El número de vértices de un cubo en dimensión n es 2^n.
Primero, unimos la cara superior con la inferior. Se obtiene una especie de "rueda de troncomóvil". Después se unen los discos laterales de la rueda. Se obtienen dos toroides, uno adentro de otro. Sólo falta unir la cara interna del toroide interno con la cara externa del toroide exterior. Esto no se puede hacer en tres dimensiones, así es que al unirlas, se obtiene una figura de cuatro dimensiones. Simplemente se unen las superficies por medio de otra dimensión.
Si uno "volara" adentro de ese hipertoroide, si uno fuera de frente, regresaría al mismo punto por atrás. Si uno fuera hacia la derecha, por la izquierda; hacia arriba, por abajo.
Grafiqué una representación en Â3 (tres dimensiones) de este hipertoroide con el archivo TORUS.MTH para Derive.
Hipertoroide
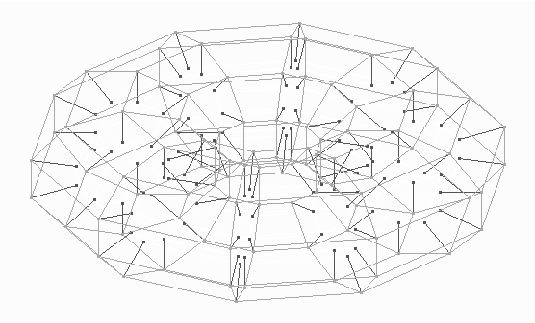
Cabe mencionar que las líneas que unen al toroide exterior con el
interior representan el espacio de cuatro dimensiones que en realidad los une.
Ahora, ¿qué sucede si se "cicla" un hipercubo? Se obtiene una representación gráfica de un espacio de cuatro dimensiones cíclico. Si consideramos al tiempo como una cuarta dimensión, hasta cierto punto, el hipercubo ciclado se podría decir que es un tiempo cíclico.
Esta figura, a la cual llamé victoroide, es de cinco dimensiones. Una representación tridimensional se puede apreciar en el archivo TORUS2.MTH para Derive.

Victoroide
Para construirla, se hacen los mismos pasos que con las figuras anteriores: se van uniendo las caras del hipercubo hasta que sus 16 vértices queden reducidos a un punto. Las líneas que se salen por arriba, se juntan con las que salen por abajo, lo cual no fue posible graficar por las limitaciones del manejo de memoria de Derive.
Aplicaciones
Un espacio cíclico se podría aplicar a un Juego de la Vida en tres dimensiones, para aumentar las posibilidades de interacción entre las "células". En el programa LIFE3D.EXE, hecho en Turbo Pascal, se puede apreciar esta característica, ya que se puede activar o desactivar la opción de hipertoroide, lo cual reduce las probabilidades de encontrar un "ser" estable, más o menos en un 40%.
Una representación de un tiempo cíclico se puede apreciar en el programa VICTOROI.EXE, hecho en Turbo Pascal. En la pantalla aparece un cubo con una pequeña esfera móvil en él. Cuando la esfera toca un extremo del cubo, aparece por el contrario. El tiempo es tomado como vector, pero con movimiento constante y uniforme. El tiempo también es cíclico, pues al llegar a 10 segundos, el cronómetro se reinicializa. En sí, la pequeña esfera está viajando por un victoroide.
En graficación estas herramientas resultan muy útiles, ya que simplifican mucho los métodos convencionales y mejoran la calidad de las imágenes, con variedades u otras figuras topológicas.
Para poder hacer cualquier simulador de física, matemáticas, biología, química o áreas afines, es necesario tener en cuenta estas características, ya que en muchos casos optimiza el funcionamiento del simulador. Ahorra muchos recursos de la máquina utilizar estos métodos, que tratar de emplear un espacio mucho mayor para tener cierta libertad al simular.
La Topología, aunque tiene poco tiempo de existir, tiene muchas más aplicaciones y usos que los explicados, lo cual dificulta su explicación completa, ya que estos son muy complicados y requieren de conocimientos matemáticos avanzados. Haciendo este trabajo accesible a la mayor cantidad de gente posible, me limito a estas aplicaciones, ya que estas son de lo más variadas. Investigando estos datos, me encontré con esta fascinante idea:
Propuesta
Bien, supongamos ahora que el Universo es un tiempo cíclico.
El universo se encuentra en expansión relativa, ya que cuando la materia de este en expansión se alejara más del centro del universo, en realidad se acercaría más y más al punto formado por la unión de los vértices.
Nosotros, que sólo percibimos tres dimensiones, vemos las distancias en línea recta, cuando en realidad, estas se "doblan", y se encontrarán cuando nosotros pensamos que están en su punto más lejano.
Así, la materia otra vez reunida en el punto donde se unen los vértices, se acumulará otra vez, y se dará otro Big Bang, comenzando el tiempo de nuevo.
Entonces, el punto donde se unen los vértices del nuevo victoroide será el centro del victoroide anterior.
Esto, por más fantasioso que parezca, explica condiciones que los modelos actuales del universo no pueden, y explica congruentemente lo que estos modelos ya incluyen.
Stephen Hawking, uno de los físicos más sobresalientes de este siglo, ya tenía un modelo parecido a este, en el sentido de que era cíclico. Él lo describe como una superficie de una esfera, pero en cuatro dimensiones, en vez de dos. Si uno camina por la superficie de una esfera, llegará al mismo punto.
Mi modelo es muy parecido a este en ese aspecto. Los dos son cíclicos, pero con este nuevo modelo se puede explicar el porqué de la uniformidad de la radiación de fondo.
La radiación de fondo fue descubierta en 1965 por Arno Penzias y Robert Wilson. Esta es una señal de microondas que es constante, en todas direcciones, día y noche, todos los días del año; lo cual indica que viene de fuera de nuestra galaxia. La radiación nunca varía más de una parte en diez mil, lo cual nos hace suponer que se encuentra en todo el Universo. Según la teoría del Big Bang, esta radiación es lo que permanece del principio del Universo. ¿Pero porqué es tan constante esta radiación, tanto en la dirección en la que nos expandemos en el universo, como de la que venimos?
Esta pregunta sólo se puede explicar hasta ahora con un Universo cíclico.
Al momento del Big Bang, Esta radiación viajó tanto hacia "afuera", como hacia "adentro", esta última radiación llegando por el infinito. Esto explica el porqué la radiación parece ser la misma en todas las partes del Universo.
Conclusiones
Al presentarse estas aplicaciones para los espacios y tiempos cíclicos se pueden entrever muchas más, como espacios y tiempos no orientables.
La Topología es una de las ramas de las Matemáticas más jóvenes y con mayores avances en los últimos años. Por lo tanto, todavía hay mucho por desarrollar en esta área, a lo cual se abocó este trabajo.
Como todas las ciencias exactas, la Topología simplifica los problemas a los que nos enfrentamos, y dado que estos problemas van casi siempre de la mano con las computadoras, es importante conocer que existen las soluciones.
Bibliografía
--Spivak, Michael. "Cálculo en Variedades". Ed. Reverté. 1988.
--Hawking, Stephen W. "Historia del Tiempo: Del big bang a los agujeros negros". Alianza Editorial. 1988.
--Comway, John. "The Game Of Life." 1970.
--Peterson, Ivars. "Islands of Truth". 1990.
--Peterson, Ivars. "The Mathemathical Tourist". 1988.
--Dewney, A. K. "Computer Recreations". Scientific American. January, 1990.
--Pérez-Enríquez, Raúl. "Las Aventuras se El Taquión por el Espacio-Tiempo". Ed. UNISON. 1997.
--Croom, Frederick. "Introduction to Topology". 1989.
--Francis, G. K. "A Topological Picturebook". 1987.
--Firby, P. A. and Gardnier, C. F. "Surface Topology". 1982.
--Barr, Stephen. "Experiments In Topology". 1972.
--Weeks, Jeffrey. "The Shape of Space". 1985.
--Stewart, Ian. "The Problem of Mathematics". 1987.