To be or not to be,
A multidimensional logic approach
Carlos Gershenson
"To be AND not to be,
that is the dimension..."
Parmenides in his ontologic poem said that the correct way is of "the Being that is" or the "not Being that isn't". And fools they who follow the wrong way of the "Being that isn't" or of the "not Being that is". Well, we won't say he was wrong. For now, we will say that he was incomplete (as we will probably be in a few centuries...), and we'll get back to this incompleteness later. Now we would say that it is necessary to follow the wrong way also.
For example, take a ball which has one hemisphere black and one white. If you see it from one perspective, you would see it is white. If you see it from another, it is black, or 31.7% white, 68.3% black, etc. If you grab the ball and you see it from all perspectives, you can say that it is black AND white. This seems very simple. Well, the same thing may be applied to the Being.
But first let's see another example. The fact that you crashed your car makes you feel bad. The fact that you met the woman of your life by crashing your car against hers makes you feel good (not that you don't care for your car). So it would be perfectly normal that you say you feel good AND bad. But you would say that you felt more goodness than badness, so let's agree that there are different degrees for feeling good and bad, different degrees for truth and lies. Well, we're talking fuzzy here (Zadeh, 1965). The same will be applied for the Being. For example, you can say that your computer exists. But you can't prove it rationally (only empirically. We'll get back to this later too). Most of us will believe it exists, though. The same thing happens for existence of psychic powers, aliens or the chupacabras (let's avoid god as long as possible...). You can't prove their existence rationally. But some people believe in them. And you can't say they're absolutely wrong because you can't prove their non-existence. Then, there are some people who believe in them. So we could say (empirically) that your computer has a higher degree of existence than that good old green Wrysk Terskel of Rigel IV. But we can't prove the existence or non-existence of neither. We can say (I believe) that more people believe in the existence of your computer than in the existence of spotty Mr. Terskel.
All this can be represented nicely by Possible World Semantics (Hintikka, 1962), in which there is a set of worlds W in which each world wi contains a possible scenario. An agent believes q if q is true for at least one of his worlds. An agent knows q if q is true in all of his worlds. Let's extrapolate this idea of Artificial Intelligence to us. The only problem is that in an AI system, W is finite. And our universe seems to be infinite (or at least if acts like it would be as long as we don't find it's limits).
So, all our worlds can't comprehend the whole universe (or can something finite contain something infinite...? we don't believe so). Since we belong to the universe, we can't say that something is true in all our worlds, because we can't perceive them all. So we can't say that we know anything. Even if it is true in all our worlds, we don't know if it is also true in the rest. This leaves us only with beliefs. Well, this is a new version of the "I only know I know nothing" of Heraclitus, Metrodorus, Socrates, and many others. Note that also something that is false in all our worlds, can't assure us that it will also be false in all the universe.
Let's now get back to our incompleteness statement about Parmenides. As we said, we can't say he was absolutely wrong. For all his wi's in his W, his thoughts were true. The same happened to Newton. You can't say that the Law of Gravity is absolutely wrong. It was true in all of Newton's W, but it is not in our relativistic wi's. We say the same for multidimensional logic (Gershenson, 1998). Right now it is valid in all our W. But we believe it won't in future W's. So, we won't say that Parmenides was wrong, just less complete than we are. Notice that W's vary from person to person, and a person's W changes through time.
Following this way, we could say that q has a higher truth value than r if it is true in more wi's than r. Getting fuzzy, q has a higher truth value than r if the sum of all truth values of q is higher than the sum of all the truth values of r. Going multidimensional, you can project the multidimensional value of q and r in FL and go the fuzzy way. Note that this applies only for one W at a time.
Before we go further, let's finish with our last statement about reason. Let's remember Gödel's theorem. He proved, that any system based in axioms, is incomplete. We can also see that a system can't prove it's validity by itself. This can be seen as trying to prove mathematics with mathematics. You need a starting point (axiom(s)) or else all your definitions will become recursive. But then, how can you prove the axioms? You need a meta system. But this will also will have it's axioms, and so on. What we are trying to say, is that we can't prove that our reason is valid rationally. Empirically, it works (I believe) most of the time, but this doesn't assures me that my reason is right. For example, I can believe that a fair lady isn't wearing any underwear (and there's only one way to prove it...). You can believe that Wrysk stopped last afternoon for tea and gave me funny stuff. Someone can believe in god (sorry, couldn't keep back any longer), and there is no way that you can prove him it's non existence with reasons, and the opposite for a non-believer. I believe that I am sitting in a chair, but I can't prove that my senses don't fool me. I also believe I exist, but I can't prove it. Maybe I'm a Replicant and my memories were implanted yesterday, and before I didn't existed. Maybe I'm a Hitler's clone, but no one has told me about it yet. This last two I don't believe, but I can't prove their falseness. So, we can't prove all these, and I can only believe in them. This could mean that faith (not religious, but the part of our minds which does the believing (which contains religious)) is a meta system of reason. Well, it is clear that I can't prove this faith... We could say that we have to believe that our reason is correct to then reason. I believe, therefore I think, therefore I am.
Now let's get way back to our black and white ball example. We said the
same example could be applied to the Being. Let's say that we all see the ball from
different perspectives, just as everyone sees the universe from different perspectives.
You can't see the complete ball, as we can't see the universe completely. For me, the ball
is all black, for you is half black and half white, for Wrysk it's 3/4 white, 1/4 black.
Who's got the most complete truth? Well, I believe I don't know. For example, getting an
average wouldn't be quite correct. Just suppose 80% of the people are viewing the ball
from where I am seeing it. Or in other words, not always the majority is correct (let's
say more complete). Well, having this kinds of uncertainties, how can we say if
the fair lady is wearing underwear? (All right, no more underwear examples). How
can we answer the following:
A believes in god and B doesn't.
Does god exist?
Well, since we can't say which beliefs are more valid, we can't say that god doesn't exist, nor that he exists. Let's say then he exists AND don't exists. Let's return to the ball. A sees only black, B sees only white (maybe it is a hyper sphere with other colours in other spaces). What can we say about the ball? This is where multidimensional logic (Gershenson, 1998) is useful. Let's say the ball is 100% black, 100% white (if it hasn't solution, give it another dimension!). If b is a multidimensional logic variable (mdlv) (black, white), we can give it the vector (1,1). Similarly, we can define a mdlv g (god exist, god doesn't exists), which would acquire also the vector (1,1) for the A and B example.
Let's define a bidimensional logic variable which represents (Being, not Being).
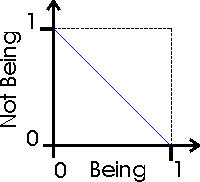
The blue line which goes form (0,1) to (1,0) represents where there's no contradiction. This is where the value of Being complements the value of not Being and vice versa (their sum is 1).
Here we can see the ways of Parmenides. For the Being that is, we take the Being axis (B), and we see that it would have a value of 1, because of the subject Being. We go to the not Being axis (NB), and we see it would have a value of 0, because of the verb is. So it would be represented by the vector of (1,0). Similarly, we can see that the not Being that not is would be represented by the vector (0,1). The not Being that is would be represented by (0,0) and the Being that not is by (1,1), or vice versa, since they're equivalent.
We believe that the frontier of the square (0,0),(0,1),(1,1),(1,0)
cannot be reached in practice. This is, returning to Possible World Semantics, that for we
could say that something has a Being value of 1 (complete), it would have to Be in all the
universe. And we can't say that because we don't know all the wi's in 
.
The same for not Being. For something to have a not Being value of 1, it would have to not
Be in all the universe. And since the Being 1 is equivalent to the not Being 0 and vice
versa, we can't reach the frontier. As a limit, we can approach "as much as we
want", but we will never reach the frontier (unless the universe is finite). All this
means that everything has Being and not Being values different from 0 or 1. This is,
everything is, and isn't... at a certain degree. (this doesn't implies necessarily
contradiction). Hope that now "Nothing is something" (not Being is) is
clearer.
But why stop in two dimensions?. Let's define a mdvl b1(Being, not Being, Being-not Being, ~Being-~not Being). These last two can be obtained with the degree of contradiction of Being and not Being. And we can see that they are equivalent. So we also could simplify defining a mdlv b2(Being, not Being, Being-not Being). In these dimensions, we can represent the Being that is and isn't, the not Being that is and isn't, etc. For making things easier, B stands for Being, NB for not Being, and ~ for negation. We can define a mdlv b3 basing in b2 (B, NB, BNB, NBB, BBNB, NBBNB, BNBBNB, NBNNBNBNB), which can easily be simplified by equivalences as a mdlv b4 (B, NB, BNB, BNBBNB). And so on, and so on...
This why it was named multidimensional logic in the first place. We can see that a higher dimensional logic can be obtained by converting the vertexes of a certain dimensional logic into the axes of the higher. Unidimensional logic (fuzzy) is obtained by making an axis of the single vertex of zero-dimensional logic. Bidimensional logic can be obtained by making axis of FL's vertexes, and so on. Note that equivalence reduces the dimensions significantly. It is similar as the number of vertexes you need to obtain a n-cube and an n-T. Without using equivalences, you get a 2^n logic when simplifying with equivalences you could stay with a n+1 logic.
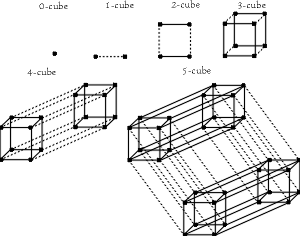
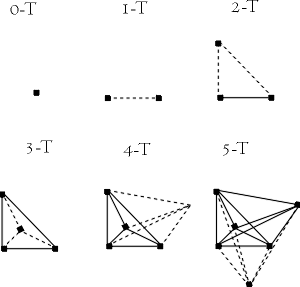
Finally, let's recapitulate all the important ideas we have mentioned:
This obviously also applies for multidimensional logic. We can't say it
will be true in all . We can't really prove that it is right or wrong because we
can't even prove if we exist.
References
E-mail: cgg
unam.mx
https://bingweb.binghamton.edu/%7Ecgershensong/unamjlagunez/mdl/be.html